БСЭ БСЭ - Большая Советская Энциклопедия (МЕ)

На основе М. с. м. возник целый ряд частных, охватывающих лишь отдельные разделы физики или отрасли техники, систем единиц и отдельных внесистемных единиц . Развитие науки и техники, а также международных связей привело к созданию на основе М. с. м. единой, охватывающей все области измерений, системы единиц — Международной системы единиц (СИ), которая уже принята в качестве обязательной или предпочтительной многими странами.

Лит.: Исаков Л. Д., На все времена, для всех народов, П., 1923; Бурдун Г. Д., Единицы физических величин, М., 1967; Широков К. П., 50-летие метрической системы в СССР, «Измерительная техника», 1968, № 9; Stille U., Messen und Rechnen in der Physik, Braunschweig, 1961.

Метри'ческие кни'ги,в дореволюционной России реестры, в которых регистрировались акты гражданского состояния . После Октябрьской революции 1917 М. к. велись до принятия в 1918 Кодекса законов об актах гражданского состояния. В СССР записи о браке, рождении, смерти совершаются в актовых (реестровых) книгах в органах ЗАГСа.

Метри'ческий те'нзор,совокупность величин, определяющих геометрические свойства пространства (его метрику). В общем случае риманова пространства n измерений метрика определяется заданием квадрата расстояния ds 2 между двумя бесконечно близкими точками ( x 1, x 2,..., x n ) и ( x 1 + dx 1, x 2 + dx 2,..., x n + dx n ):

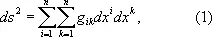
где x 1, x 2,..., x n — координаты, g ik — некоторые функции координат. Совокупность величин g ik образует тензор второго ранга, который и называется М. т. Этот тензор симметричен, т. е. g ik= g ki . Вид компонент М. т. g ik зависит от выбора системы координат, однако ds 2 не меняется при переходе от одной координатной системы к другой, т. е. является инвариантом относительно преобразований координат. Если выбором системы координат можно привести М. т. к виду

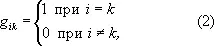
то пространство является плоским, евклидовым пространством (для трёхмерного пространства ds 2= dx 2 + dy 2 + dz 2 , где x 1= х, x 2= у, x 3= z — декартовы прямоугольные координаты). Если никаким преобразованием координат нельзя привести М. т. к виду (2), пространство является искривленным и кривизна пространства определяется М. т.

В теории относительности М. т. определяет метрику пространства-времени .

Лит . см. при статьях Римановы геометрии , Относительности теория , Тяготение .

Г. А. Зисман.

Метри'ческое простра'нство,множество объектов (точек), на котором введена метрика . Всякое М. п. является топологическим пространством ; за окрестности в нём принимаются всевозможные открытые шары [при этом открытым шаром радиуса R с центром в точке x 0 называется совокупность всех точек х , для которых расстояние r( х, x 0 ) < R ]. Топология одного и того же множества может быть различной в зависимости от метрики, введённой на нём. Например, на множестве вещественных функций, определённых и непрерывных на отрезке [ a, b ] числовой оси, можно ввести две метрики:

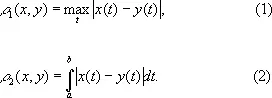
Соответствующие М. п. обладают разными топологическими свойствами. М. п. с метрикой (1) является полным [для любой последовательности его точек { x n } такой, что r 1( x n, x m ) ® 0 При n, m ® ¥, найдётся элемент x 0 М. п., являющийся пределом этой последовательности]; М. п. с метрикой (2) этим свойством не обладает. В М. п. можно вводить фундаментальные понятия анализа: непрерывность отображения одного М. п. в другое, сходимость, компактность и т.д. Понятие «М. п.» было введено М. Фреше в 1906.

Лит.: Александров П. С., Введение в общую теорию множеств и функций, М. — Л. 1948; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 3 изд., М., 1972; Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965.

В. И. Соболев.

Метри'ческое стихосложе'ние,квантитативное стихосложение, стихосложение , основанное на упорядоченном чередовании долгих и кратких слогов. Употребительно в языках, в которых долгота и краткость гласных имеют смыслоразличительное значение. Наибольшее развитие получило в араб. стихосложении (см. Аруз ) и в античном. В античном М. с. единицей долготы в стихе служит доля — мора ; краткий слог (È) считается равным одной море, долгий слог (—) — двум. Повторяющаяся группа долгих и кратких слогов называется стопой . Важнейшие стопы: трёхдольные (трёхморные) — ямб (È —), хорей, или трохей (—È), трибрахий (È È È); четырёхдольные — спондей (— —), дактиль (—È È), анапест (È È —); пятидольные — бакхий с антибакхием (È — —, — — È), амфимакр (—È —) и 4 пеона (—È È È, È — È È, È È — È, È È È —); шестидольные — молосс (— — —, хориямб (—ÈÈ —), антиспаст (È — — È) и 2 ионика (È È — —, — — È È); семидольные — 4 эпитрита (È — — —, — È — —, — — È —, — — — È). В каждой стопе различается сильное место — арсис, или икт (обычно долгий слог), и слабое место — тесис (обычно краткие слоги); сильные места выделяются при произношении особым ритмическим ударением, фонетическая природа которого не совсем ясна. Короткие трёхдольные стопы (иногда и четырёхдольные) обычно объединяются в пары — диподии , где одна из стоп несёт усиленное ритмическое ударение. Стих, как правило, состоит из одинаковых стоп и носит соответствующее название: дактилический гекзаметр (6 стоп), ямбический триметр (3 диподии) и т.п. Однако в таком стихе равнодольные стопы могут заменять друг друга: так, в дактилическом гекзаметре стопа дактиля (—È È) может заменяться стопой спондея (— —). При перемене темпа произнесения могут заменять друг друга даже неравнодольные стопы: так, в ямбическом триметре ямб (È —) может заменяться убыстрённым спондеем (— —) и даже убыстрённым дактилем и анапестом (—È È,È È —). Всё это создаёт чрезвычайное богатство метрических вариаций в пределах постоянного такта — стопы. Метрическое разнообразие стиха усиливается использованием передвижной цезуры — словораздела, который рассекает одну из средних стоп и делит стих на 2 полустишия — одно с нисходящим ритмом (—È È...), другое с восходящим (È È —...).

Такие стихи употреблялись в эпосе и драме. В лирике наряду с ними употреблялись более сложно построенные стихи с переменными стопами — логаэды : здесь периодичность повторения стоп проявляется не в пределах одного стиха, а в пределах группы стихов — строфы (алкеева строфа, сапфическая строфа и пр.), подчас очень большого объёма и сложности (например, в хоровой лирике у древне-греческого поэта Пиндара). М. с. в античной литературе зародилось в древнейшие времена, когда поэзия была ещё нераздельна с музыкой; получила теоретическую разработку, когда стих отделился от пения; держалась, пока в лат. и греч. языках различались долгота и краткость слогов, а потом в средние века уступила место силлабическому и тоническому стихосложению, хотя по традиции греч. и лат. стихи в системе М. с. писались ещё долго. Подлинное звучание античных стихов в тоническом стихосложении невоспроизводимо; в т. н. «переводах размером подлинника» принято передавать ударными слогами — ритмические ударения, а безударными слогами — слабые места стоп.