БСЭ БСЭ - Большая Советская Энциклопедия (МЕ)

Лит.: Циолковский К. Э., Собр. соч., т. 2, М., 1954; Мещерский И. В., Работы по механике тел переменной массы, 2 изд., М., 1952; Космодемьянский А. А., Механика тел переменной массы, ч. 1, [М.], 1947; его же, Курс теоретической механики, 3 изд., ч. 2, М., 1966; Миеле А., Механика полета (теория траекторий полёта), пер. с англ., М., 1965.

А. А. Космодемьянский.

Меха'ники уравне'ния канони'ческие,уравнения Гамильтона, дифференциальные уравнения движения механической системы, в которых переменными, кроме обобщённых координат q i, являются обобщённые импульсы p i ; совокупность q i и p i называется каноническими переменными. М. у. к. имеют вид:

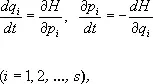
где H ( q i, p i, t ) — функция Гамильтона, равная (когда связи не зависят от времени, а действующие силы потенциальны) сумме кинетической и потенциальной энергий системы, выраженных через канонические переменные, s — число степеней свободы системы. Интегрируя эту систему обыкновенных дифференциальных уравнений 1-го порядка, можно найти все q i и p i как функции времени t и 2 s постоянных, определяемых по начальным данным.

М. у. к. обладают тем важным свойством, что позволяют с помощью т. н. канонических преобразований перейти от q i и p i к новым каноническим переменным Q i ( q i, p i, t ) и P i ( q i, p i, t ), которые тоже удовлетворяют М. у. к., но с другой функцией H ( Q i, P i, t ). Таким путём М. у. к. можно привести к виду, упрощающему процесс их интегрирования. М. у. к. используются, кроме классической механики, в статистической физике, квантовой механике, электродинамике и др. областях физики.

С. М. Тарг.

Меха'нико-математи'ческое образова'ние,система подготовки специалистов высшей квалификации для научно-исследовательской и преподавательской работы в области математики, механики и смежных с ними отраслей науки, техники, экономики, промышленности и сельского хозяйства. В СССР принято различать общее математическое образование, которое даёт средняя общеобразовательная школа , где основы математической науки изучаются с 1-го класса, специальное и вспомогательное М.-м. о.

Специальное М.-м. о. дают механико-математические и физико-математические факультеты (отделения) университетов и педагогических институтов. В России специальное М.-м. о. впервые стало осуществляться в Академии, университете в Петербурге (основан в 1726), затем в Московском университете (1755) и Учительской гимназии в Петербурге (1803). Уже в 18 в. из университетов вышли видные деятели русской математической науки и просвещения: С. Е. Гурьев, С. Я. Румовский, Т. Ф. Осиповский и др.; на них большое влияние оказали педагогические взгляды Л. Эйлера . В 19 в. специальное М.-м. о. получило развитие в Казанском, Харьковском, Киевском, Петербургском, Новороссийском (Одесском), Тартуском (Дерптском) и др. университетах, воспитанниками которых были Н. И. Лобачевский, М. В. Остроградский, П. Л. Чебышев, Н. Е. Жуковский, А. М. Ляпунов и др., ставшие основоположниками новых отраслей и разделов математики и механики и способствовавшие совершенствованию общего и специального М.-м. о. в России. В начале 20 в. отечественная математическая школа была представлена такими учёными, как А. М. Ляпунов, А. А. Марков, А. Н. Крылов (Петербург), Н. Е. Жуковский, Д. Ф. Егоров, Н. Н. Лузин, С. А. Чаплыгин (Москва), С. Н. Бернштейн (Харьков) и др. Физико-математические факультеты университетов готовили преимущественно преподавателей математики для гимназий, реальных училищ, высших и средних специальных учебных заведений. Университетские курсы достаточно полно отражали содержание и уровень развития математики и механики того времени. В этот период механика составляла естественную часть специального М.-м. о.

Уже в первые годы Советской власти университеты стали крупнейшими учебными и научными математическими центрами. Индустриализация страны потребовала приближения математической подготовки специалистов к нуждам развивающейся промышленности. В начале 30-х гг. университетское М.-м. о. подверглось существенной реорганизации. Были выделены механические специальности, в первую очередь по аэродинамике, гидродинамике, теории упругости, общей механике; в учебных планах нашли отражение современные научные идеи (в частности, функциональный анализ, тензорная геометрия и др.); во многих университетах физико-математические факультеты разделены на механико-математические и физические, в некоторых — созданы научно-исследовательские институты механики и математики. В 50—60-е гг. в университетах были организованы факультеты вычислительной математики, кибернетики, автоматических систем управления, в ряде втузов — факультеты прикладной математики. Университеты готовят математиков и механиков-теоретиков для различных отраслей народного хозяйства, преподавателей средней и высшей школы, сотрудников научно-исследовательских учреждений. Студенты-математики, помимо общенаучных (в т. ч. и математических — математический анализ, высшая алгебра, аналитическая геометрия и др.) дисциплин, изучают теоретическую механику, теорию функций комплексного переменного, теорию функций действительного переменного и функциональный анализ, математическую логику, теорию вероятностей и математическую статистику, дифференциальные уравнения, математическую физику и др. В 50-е гг. в учебные планы введены курсы программирования для ЭВМ, усилена подготовка по вычислительной математике; в большинстве университетов созданы вычислительные центры. Значительно расширилась подготовка специалистов в области механики, особенно в связи с исследованием космоса, развитием автоматики и автоматических систем управления, необходимостью исследования механических свойств как старых, так и новых синтетических материалов. Студенты-механики получают основательную математическую подготовку (близкую той, которую получают студенты-математики), изучают теорию упругости, теорию пластичности, гидро- и аэродинамику, сопротивление материалов и др. Учителей математики для средней школы в основном готовят педагогические институты. В учебных планах значительное место занимают общематематические, общепедагогические и методические дисциплины. Студенты изучают основания арифметики и геометрии, теорию вероятностей, математическую логику, курс математических машин и программирование для ЭВМ, общую физику и астрономию. Большое внимание уделяется курсу элементарной математики, методике преподавания математики, педагогической практике в школе. В некоторых педагогических институтах подготовка учителей ведётся по профилям: математика — физика, математика — программирование, математика — черчение. Сроки обучения на механико-математических специальностях: 5—6 лет — в университетах, 4—5 лет — в педагогических институтах. В 1974 подготовка специалистов с М.-м. о. велась по специальностям: математика (58 университетов — 38,2 тыс. студентов, приём — 8,8 тыс. человек, выпуск — 5,6 тыс. человек, и около 200 педагогических институтов — 129,9 тыс. студентов, приём — 27,1 тыс. человек, выпуск — 23,3 тыс. человек); механика (свыше 20 университетов — 4,3 тыс. студентов, приём — около 1 тыс. человек, выпуск — 0,7 тыс. человек); прикладная математика (свыше 60 вузов различного профиля и университетов — 23,9 тыс. студентов, приём — 7,4 тыс. человек, выпуск — 1,9 тыс. человек). В вузах, научно-исследовательском институте математики и механики АН СССР, в академиях союзных республик, АПН СССР организована аспирантура для подготовки научных кадров в области математики и механики.