БСЭ БСЭ - Большая Советская Энциклопедия (МЕ)
- Название:Большая Советская Энциклопедия (МЕ)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (МЕ) краткое содержание
Большая Советская Энциклопедия (МЕ) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
В. Г. Афонин.
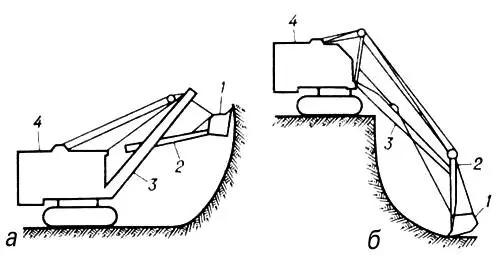
Механическая лопата: а — прямая; б — обратная; 1 — ковш; 2 — рукоять; 3 — стрела; 4 — кузов.
Механические музыкальные инструменты
Механи'ческие музыка'льные инструме'нты,инструменты, снабженные техническими приспособлениями для исполнения зафиксированных на дисках произведений или наигрышей без непосредственного участия музыкантов. М. м. и. бывают самых различных конструкций и форм — от маленьких примитивных табакерок, музыкальных шкатулок , часов-будильников до сложных по устройству стационарных напольных часов, полифонов, оркестрионов , башенных курантов , «озвученных» карет. Первые сведения о М. м. и. относятся к 16 в. Особенно много систем М. м. и. появилось, в том числе и в России, в конце 19 — начале 20 вв. Применялись они в трактирах, ресторанах, мещанско-купеческом быту. Широкое распространение в это время получила шарманка . С появлением граммофона, а затем радиомагнитофонной аппаратуры М. м. и. вышли из употребления. См. также Механическое фортепьяно .
Механические свойства материалов
Механи'ческие сво'йства материа'лов,совокупность показателей, характеризующих сопротивление материала воз действующей на него нагрузке, его способность деформироваться при этом, а также особенности его поведения в процессе разрушения. В соответствии с этим М. с. м. измеряют напряжениями (обычно в кгс/мм 2 или Мн/м 2 ) , деформациями (в %), удельной работой деформации и разрушения (обычно в кгс × м/см 2 или Мдж/м 2 ) , скоростью развития процесса разрушения при статической или повторной нагрузке (чаще всего в мм за 1 сек или за 1000 циклов повторений нагрузки, мм/кцикл ) . М. с. м. определяются при механических испытаниях образцов различной формы.
В общем случае материалы в конструкциях могут подвергаться самым различным по характеру нагрузкам ( рис. 1 ): работать на растяжение, сжатие, изгиб , кручение , срез и т. д. или подвергаться совместному действию нескольких видов нагрузки, например растяжению и изгибу. Также разнообразны условия эксплуатации материалов и по температуре, окружающей среде, скорости приложения нагрузки и закону её изменения во времени. В соответствии с этим имеется много показателей М. с. м. и много методов механических испытаний. Для металлов и конструкционных пластмасс наиболее распространены испытания на растяжение, твёрдость , ударный изгиб; хрупкие конструкционные материалы (например, керамику, металлокерамику) часто испытывают на сжатие и статический изгиб; механические свойства композиционных материалов важно оценивать, кроме того, при испытаниях на сдвиг.
Диаграмма деформации.Приложенная к образцу нагрузка вызывает его деформацию . Соотношения между нагрузкой и деформацией описываются т. н. диаграммой деформации ( рис. 2 ). Вначале деформация образца (при растяжении — приращение длины D l ) пропорциональна возрастающей нагрузке Р , затем в точке n эта пропорциональность нарушается, однако для увеличения деформации необходимо дальнейшее повышение нагрузки Р ; при D l > D l вдеформация развивается без приложения усилия извне, при постепенно падающей нагрузке. Вид диаграммы деформации не меняется, если по оси ординат откладывать напряжение
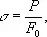
а по оси абсцисс — относительное удлинение
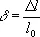
( F 0 и l 0 — соответственно начальная площадь поперечного сечения и расчётная длина образца).
Сопротивление материалов измеряется напряжениями, характеризующими нагрузку, приходящуюся на единицу площади поперечного сечения образца
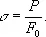
в кгс/мм 2. Напряжение
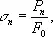
при котором нарушается пропорциональный нагрузке рост деформации, называется пределом пропорциональности. При нагрузке Р < Р n разгрузка образца приводит к исчезновению деформации, возникшей в нём под действием приложенного усилия; такая деформация называется упругой. Небольшое превышение нагрузки относительно Р n может не изменить характера деформации — она по-прежнему сохранит упругий характер. Наибольшая нагрузка, которую выдерживает образец без появления остаточной пластической деформации при разгрузке, определяет предел упругости материала:
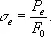
У конструкционных неметаллический материалов (пластмассы, резины) приложенная нагрузка может вызвать упругую, высокоэластическую и остаточную деформации. В отличие от упругой, высокоэластическая деформация исчезает не сразу после разгрузки, а с течением времени. Высокопрочные армированные полимеры (стеклопластики, углепластики и др.) разрушаются при удлинении 1—3%. На последних стадиях нагружения у некоторых армированных полимеров появляется высокоэластическая деформация. Высокоэластический модуль ниже модуля упругости, поэтому диаграмма деформации в этом случае имеет тенденцию отклоняться к оси абсцисс.
Упругие свойства.В упругой области напряжение и деформация связаны коэффициентом пропорциональности. При растяжении s = Еd, где Е — т. н. модуль нормальной упругости, численно равный тангенсу угла наклона прямолинейного участка кривой s = s(d) к оси деформации ( рис. 2 ). При испытании на растяжение цилиндрического или плоского образца одноосному (s 1>0; (s 2= s 3= 0) напряжённому состоянию соответствует трёхосное деформированное состояние (приращение длины в направлении действия приложенных сил и уменьшение линейных размеров в двух других взаимно перпендикулярных направлениях): d 1>0; d 2= d 3< 0. Соотношение между поперечной и продольной деформацией (коэффициент Пуассона)
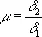
в пределах упругости для основных конструкционных материалов колеблется в довольно узких пределах (0,27—0,3 для сталей, 0,3—0,33 для алюминиевых сплавов). Коэффициент Пуассона является одной из основных расчётных характеристик. Зная m и Е , можно расчётным путём определить и модуль сдвига
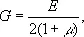
и модуль объёмной упругости
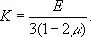
Интервал:
Закладка:
