БСЭ БСЭ - Большая Советская Энциклопедия (НА)

Лит.: Константинов Н. А., Струминский В. Я., Очерки по истории начального образования в России, 2 изд., М., 1953; Проблемы обучения и воспитания в начальной школе. Под ред. Б. Г. Ананьева и А. И. Сорокиной, М., 1960; Вопросы психологии учебной деятельности младших школьников. Под ред. Д. Б. Эльконина и В. В. Давыдова, М., 1962; Занков Л. В., О начальном обучении, М., 1963; Основные вопросы начального обучения. Сб. Под ред. А. С. Пчелко, М., 1963; Программы восьмилетней школы. Начальные классы (I—III), М., 1972; Очерки истории школы и педагогической мысли народов СССР. XVIII в. — пер. пол. XIX в., М., 1973.

П. В. Зимин.

Нача'льное усло'виепри математическом анализе процесса, состояние этого процесса в какой-либо момент времени, принятый за начальный. Если процесс описывается дифференциальным уравнением, то задача об отыскании решений по Н. у. называется Коши задачей. Для уравнения

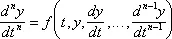
Н. у. состоит в задании

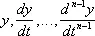
при значении t = t 0Если n = 2 и y = y ( t ) — закон движения материальной точки, то в Н. у. задаётся положение точки и её скорость в момент t = t 0. Н. у. для дифференциального уравнения с частными производными ставится аналогично. Так, для уравнения свободных колебании струны

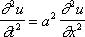
где u ( t, x ) — отклонение точки х струны в момент t от её положения покоя на оси Ox , Н. у. состоит в задании начальной формы струны

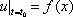
и начальных скоростей точек струны

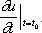
Роль времени может играть какой-либо другой аргумент; тогда Н. у. задаётся при некотором значении этого аргумента.

Начерта'тельная геоме'трия, раздел геометрии, в котором пространственные фигуры изучаются при помощи построения их изображений на плоскости, в частности построения проекционных изображений, а также методы решения и исследования пространственных задач на плоскости.

Потребность в изображениях пространственных предметов на плоскости возникла в связи с решением различных практических вопросов (например, строительство зданий и других инженерных сооружений, развитие живописи и архитектуры, техники и т.п.). Особенно большое значение имеют чертежи, получаемые проектированием (проецированием) данной фигуры на плоскость (проекционные чертежи). Практика предъявляла к таким чертежам ряд требований; важнейшие из них: 1) наглядность изображения, т. е. свойство чертежа вызывать пространственное представление изображаемой фигуры; 2) «обратимость» чертежа, т. е. возможность точного определения изображенной фигуры по чертежу; 3) простота выполнения требуемых построений; 4) точность графических решений. В способах построения изображений применяются центральное и параллельное проектирование фигуры (натуры, объекта, оригинала) на плоскость проекций (см. Проекция ) . Наибольшей наглядностью обладают чертежи, полученные способом центрального проектирования, который соответствует геометрической схеме возникновения изображений на сетчатке человеческого глаза. Однако наиболее употребительными в Н. г. являются параллельные проекции, которые более просты в построении изображений и более удобны для определения по ним натуральной фигуры. Существуют различные виды параллельных проекций; самым распространённым является способ ортогональной проекции на две или три плоскости (комплексный чертёж). Сущность этого способа заключается в следующем. Выбирают две взаимно перпендикулярные плоскости проекций П 1 и П 2 в пространстве. Плоскость П 1 располагают горизонтально; её называют горизонтально и плоскостью проекций, а плоскость П 2— фронтальной плоскостью проекций. Произвольную точку А пространства проектируют ортогонально на эти плоскости ( рис. 1 ); получают горизонтальную проекцию A 1 ( AA 1 (плоскости П 1 ) и фронтальную проекцию A 2 ( AA 2 ^ плоскости П 2 ). Три точки А , A 1 и A 2 лежат в одной (проектирующей) плоскости, перпендикулярной к линии p 12 пересечения плоскостей проекций. Горизонтальную проекцию какой-либо фигуры получают, проектируя ортогонально все точки этой фигуры на плоскость П 1 , фронтальную проекцию — на плоскость П 2 . Часто бывает полезно добавить третью проекцию фигуры — на плоскость П 3, перпендикулярную к плоскостям П 1 и П 2. Плоскость П 3, а также и проекцию на неё называют профильной. Две проекции точки А (например, A 1 и A 2 ) вполне определяют третью проекцию ( A 3 ) .

Чтобы получить чертёж, состоящий из трёх указанных проекций (комплексный чертёж), плоскости П 1 и П 3 совмещают с плоскостью П 2 («главной» плоскостью) путём вращения их вокруг линий p 12 и p 23 пересечения этих плоскостей с плоскостью П 2 ( рис. 2 ). Обычно на практике не указывается положение осей проекций p 12 и p 13 , то есть положение плоскостей проекций определяется с точностью до параллельного переноса.

Комплексный чертёж обратим, так как по нему можно определить расстояние между любыми двумя точками натуральной фигуры. Действительно, отрезок AB ( рис. 3 ) в натуре является гипотенузой прямоугольного треугольника ABB*, в котором AB* = A 1B 1, а В*В есть разность высот точек В и А, выражаемая на чертеже отрезком B 2*B 2 . Отсюда можно получить простое построение натурального отрезка

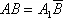
( рис. 4 ); для этого нужно построить

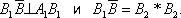
Для увеличения наглядности комплексного чертежа на проекциях фигуры устанавливают «условия видимости»: из двух точек А и В, проекции которых на какой-либо из плоскостей проекций совпадают, например A 1 º B 1 , видимой считается та, которая расположена ближе к зрителю; «невидимые» линии фигуры условно изображаются штриховыми линиями. Пример такого изображения пространственной фигуры в трёх проекциях, называется «вид спереди» (фронтальная проекция), «вид сверху» (горизонтальная проекция) и «вид слева» (профильная проекция), дан на рис. 5 .