БСЭ БСЭ - Большая Советская Энциклопедия (ОБ)

где имеется в виду положительное значение корня (так как cos х > 0 для —p/2 < х < p/2).

Обра'тно пропорциона'льные величи'ны, две величины, связанные между собой так, что с увеличением (уменьшением) одной величины в несколько раз другая уменьшается (увеличивается) во столько же раз. О. п. в. х и у связаны соотношением ху = k (то есть х = и у = , где k постоянно).

Обра'тное тре'бование,см. Регрессный иск .

Обра'тное число', число, произведение которого с данным числом равно единице. Два таких числа называются взаимно обратными. Таковы, например, 5 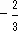и , и 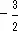и т.д. Для всякого числа а , не равного нулю, существует обратное .

Обра'тные гиперболи'ческие фу'нкции, функции, обратные по отношению к гиперболическим функциям sh х , ch х , th х ; они выражаются формулами

(*)

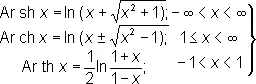(читается: ареа-синус гиперболический, ареа-косинус гиперболический, ареа-тангенс гиперболический). Эти обозначения происходят от лат. area — площадь (гиперболические функции могут рассматриваться как функции площади гиперболического сектора). Производные О. г. ф. имеют вид

,

,

.

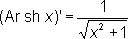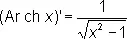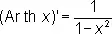Поэтому О. г. ф. часто появляются при интегрировании рациональных дробей и квадратичных иррациональностей.

О. г. ф., рассматриваемые в комплексной области, многозначны. Их однозначные ветви (главные значения) получаются, если в формулах (*) брать для логарифма его главные значения; они обозначаются ar sh z; ar ch z, ar th z. Главные значения О. г. ф. связаны с главными значениями обратных тригонометрических функций формулами

,

,

.

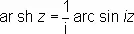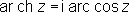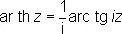Обра'тные тригонометри'ческие фу'нкции, аркфункции, круговые функции, решают следующую задачу: найти дугу (число) по заданному значению её тригонометрической функции. Шести основным тригонометрическим функциям соответствуют шесть О. т. ф.: 1) Arc sin х («арксинус x ») — функция, обратная sin х ; 2) Arc cos x («арккосинус x ») — функция, обратная cos х ; 3) Arc tg x («арктангенс x ») — функция, обратная tg х ; 4) Arc ctg x («арккотангенс x ») — функция, обратная ctg x ; 5) Arc sec x («арксеканс x ») — функция, обратная sec x ; 6) Arc cosec x («арккосеканс x ») — функция, обратная cosec x . Согласно этим определениям, например, х = Arc sin a есть любое решение уравнения sin х = a , т.е. sin Arc sin a = a . Функции Arc sin x и Arc cos x определены (в действительной области) для | х| £ 1, функции Arc tg х и Arc ctg х — для всех действительных х , а функции Arc sec х и Arc cosec х :—для | х | ³ 1; две последние функции малоупотребительны.

Так как тригонометрические функции периодические, то обратные к ним функции являются многозначными функциями. Определённые однозначные ветви (главные ветви) этих функций обозначаются так: arc sin х , arc cos x ,..., arc cosec x . Именно, arc sin х есть та ветвь функции Arc sin х , для которой — p/2 £ arc sin х £ p/2. Аналогично, функции arc cos х , arc tg х и arc ctg х определяются из условий: 0 £ arc cos х £ p, — p/2 < arc tg x < p /2 , 0 x < p. На рис. изображены графики функций у = Arc sin x , у = Arc cos x , у = Arc tg x , у = Arc ctg x ; главные Arc cos x = ± arc cos x +2p n, ветви этих функций выделены жирной линией. О. т. ф. Arc sin х ,... легко выражаются через arc sin x ,..., например

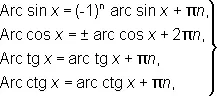
n = 0, ±1, ±2, …

Известные соотношения между тригонометрическими функциями приводят к соотношениям между О. т. ф., например из формулы

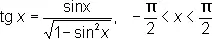
вытекает, что

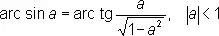
Производные О. т. ф. имеют вид

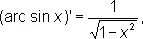
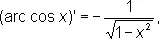
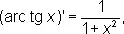
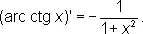
О. т. ф. могут быть представлены степенными рядами, например

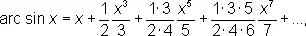
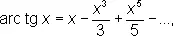
эти ряды сходятся для —1 £ x £ 1.

О. т. ф. можно определить для произвольных комплексных значений аргумента; однако их значения будут действительными лишь для указанных выше значений аргумента. О. т. ф. комплексного аргумента могут быть выражены с помощью логарифмической функции, например

.

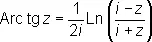Лит.: Новоселов С. И., Обратные тригонометрические функции, 3 изд., М., 1950.

Обра'тный кла'пан, устройство, пропускающее поток жидкости или газа по трубопроводу только в одном направлении и автоматически закрывающееся при перемене направления потока. Применяется в различных теплоэнергетических и технологических установках.