БСЭ БСЭ - Большая Советская Энциклопедия (ОП)

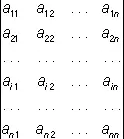
О., составленный из элементов матрицы (1), записывают в виде:

(3)

(или, сокращённо, в виде | a ik |). Для О. 2-го и 3-го порядков имеем формулы:

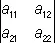= a 11 a 22– a 12 a 21,

= a 11 a 22 a 33+ a 12 a 23 a 31+ a 13 a 21 a 32– a 11 a 23 a 32– a 12 a 21 a 33– a 13 a 22 a 31.

О. 2-го и 3-го порядков допускают простое геометрическое истолкование: 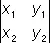равен площади параллелограмма, построенного на векторах a 1= ( x 1, y 1) и a 2= ( х 2. у 2), а 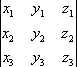равен объёму параллелепипеда, построенного на векторах a 1 = ( x 1, y 1, z 1), a 2 = ( x 2, у 2, z 2) и а 3= ( х 3, y 3, z 3) (системы координат предполагаются прямоугольными).

Теория О. возникла в связи с задачей решения систем алгебраических уравнений 1-й степени ( линейные уравнения ). В наиболее важном случае, когда число уравнений равно числу неизвестных, такая система может быть записана в виде:

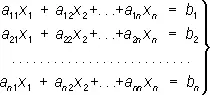(4)

Эта система имеет одно определённое решение, если О. | a ik |, составленный из коэффициентов при неизвестных, не равен нулю; тогда неизвестное x m ( m = 1, 2, ..., n ) равно дроби, у которой в знаменателе стоит О.| a ik |, а в числителе — О., получаемый из | a ik | заменой элементов m -го столбца (т. е. коэффициентов при х т ) числами b 1, b 2, ..., b n . Так, в случае системы двух уравнений с двумя неизвестными

решение даётся формулами

; .

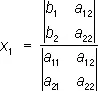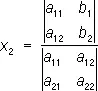Если b 1= b 2 = ..., = b n = 0, то систему (4) называется однородной системой линейных уравнений. Однородная система имеет отличные от нуля решения, только если | a ik | = 0. Связь теории О. с теорией линейных уравнений позволила применить теорию О. к решению большого числа задач аналитической геометрии. Многие формулы аналитической геометрии удобно записывать при помощи О.; например, уравнение плоскости, проходящей через точки с координатами ( x 1, y 1, z 1), ( x 2, y 2, z 2), ( х 3, y 3, z 3), может быть записано в виде:

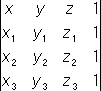= 0.

О. обладают рядом важных свойств, которые, в частности, облегчают их вычисление. Простейшие из этих свойств следующие:

1) O. не изменяется, если в нём строки и столбцы поменять местами:

= ;

2) О. меняет знак, если в нём поменять местами две строки (или два столбца); так, например:

= – ;

3) О. равен нулю, если в нём элементы двух строк (или двух столбцов) соответственно пропорциональны; так, например:

= 0;

4) общий множитель всех элементов строки (или столбца) О. можно вынести за знак О.; так, например:

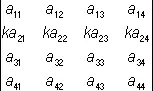= k ;

5) если каждый элемент какого-нибудь столбца (строки) О. есть сумма двух слагаемых, то О. равен сумме двух О., причём в одном из них соответствующий столбец (строка) состоит из первых слагаемых, а в другом — из вторых слагаемых, остальные же столбцы (строки) — те же, что и в данном О.; так, например:

= + ;

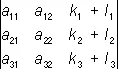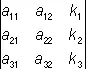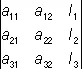6) О. не изменяется, если к элементам одной строки (столбца) прибавить элементы другой строки (другого столбца), умноженные на произвольный множитель; так, например:

= ;

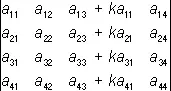7) О. может быть разложен по элементам какой-либо строки или какого-либо столбца. Разложение О. (3) по элементам i -й строки имеет следующий вид:

= a i 1 A i 1+ a i 2 A i 2+ ...+ a inA in .

Коэффициент A ik , стоящий при элементе a ik в этом разложении, называется алгебраическим дополнением элемента a ik . Алгебраическое дополнение может быть вычислено по формуле: A ik = (–1) i + k D ik , где D ik — минор (подопределитель, субдетерминант), дополнительный к элементу a ik , то есть О. порядка n- 1, получающийся из данного О. посредством вычёркивания строки и столбца, на пересечении которых находится элемент a ik . Например, разложение О. 3-го порядка по элементам второго столбца имеет следующий вид:

= –a 12 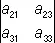+ a 22 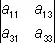– a 32 .

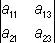Посредством разложения по элементам строки или столбца вычисление О. n -го порядка приводится к вычислению n определителей ( n - 1)-го порядка. Так, вычисление О. 5-го порядка приводится к вычислению пяти О. 4-го порядка; вычисление каждого из этих О. 4-го порядка можно, в свою очередь, привести к вычислению четырёх О. 3-го порядка (формула для вычисления О. 3-го порядка приведена выше). Однако, за исключением простейших случаев, этот метод вычисления О. практически применим лишь для О. сравнительно небольших порядков. Для вычисления О. большого порядка разработаны различные, практически более удобные методы (для вычисления О. n -го порядка приходится выполнять примерно n 3арифметических операций).