БСЭ БСЭ - Большая Советская Энциклопедия (ОР)

Координаты ( x , у ) и ( х' , у' ) в двух прямолинейных системах координат на плоскости связаны соотношениями

х'= a 11x + a 12y + b 1

y’ = a 21x + a 22y + b 2 ,

где определитель

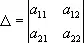
отличен от нуля. Системы координат ( х , у ) и ( х' , у' ) ориентированы одинаково, если D>0, и противоположно, если D<0. Это обстоятельство можно использовать для строгой аналитической теории О. на плоскости. Легко видеть, что множество S всех прямолинейных систем координат распадается на два подмножества S’ и S’’ так, что в пределах S’ (и в пределах S’’ ) все системы координат связаны преобразованиями с D>0, а любая система координат из S’ связана с системой координат из S’’ преобразованием с D<0. Выбрать О. плоскости - это и значит выбрать одно из множеств S' или S” . Выбор О. на плоскости определяет знак расположенных на плоскости углов и площадей, ограниченных ориентированными замкнутыми кривыми. Например, формула

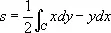
площади s , ограниченной замкнутой кривой с , ориентированной в направлении, указанном стрелкой, в случае правой системы координат ( рис. 5 и 6 ) приведёт к положительной площади для фигур рис. 2 и 4 и к отрицательной — для фигуры на рис. 3 . Наоборот, в левой системе координат ( рис. 7 ) вычисленные по формуле площади s фигуры на рис. 3 будут положительны, площади же фигур на рис. 2 и 4 — отрицательны.

Ориентация поверхности. Подобно тому, как была выше определена О. плоскости, может быть определена О. любой поверхности, делящей пространство на две части (например, сферы). Для этого рассматриваются куски поверхности, ограниченные простыми замкнутыми линиями. Ориентировать такой кусок поверхности — это значит выбрать определённую О. ограничивающей его кривой. Два куска поверхности называются ориентированными одинаково, если при обходе ограничивающих эти куски поверхности кривых в указанном направлении сами куски поверхности остаются с одной и той же стороны. Например, поверхности на рис. 8 и 9 двух кубов ориентированы одинаково, а поверхность третьего ( рис. 10 ) — противоположным образом. Поверхность вместе с определённой О. кусков, ограниченных простыми замкнутыми кривыми, и называют ориентированной поверхностью. Не всякая поверхность может быть ориентирована (см. Ориентируемая поверхность ). Однако поверхности, ограничивающие часть пространства, всегда принадлежат к числу ориентируемых.

Ориентация пространства. Пусть замкнутая поверхность ограничивает определённый кусок пространства. Говорят, что такая поверхность ориентирована правым образом, если куски этой поверхности, наблюдаемые снаружи, представляются ориентированными против часовой стрелки, подобно кубам на рис. 8 и 9 . Наоборот, О. замкнутой поверхности, ограничивающей кусок пространства, считается левой, если её куски ориентированы при наблюдении снаружи по часовой стрелке, подобно кубу на рис . 10 . Выбор определённой О. замкнутых поверхностей без самопересечений называется О. самого трёхмерного пространства. Т. о., существуют две О. трёхмерного пространства: правая и левая. О. пространства можно установить также при помощи выбора системы декартовых координат. Если выбраны оси координат Ox , Оу и Oz с определёнными положительными направлениями на них, то соответствующая О. пространства определяется следующим условием: рассматривается какой-либо тетраэдр ОАВС с вершиной О в начале и вершинами А , В , С соответственно на положительных лучах осей Ox , Оу и Oz ( рис. 11 , 12 ), треугольник АВС , лежащий на поверхности этого тетраэдра, ориентируется в порядке АВС (т. е. от оси Ox к оси Оу и затем к оси Oz ); этим определяется О. поверхности тетраэдра, а следовательно, и всего пространства. Выбор осей на рис. 11 соответствует правой О. пространства, выбор же осей на рис. 12 — левой О. пространства. По указанному принципу сами системы координат в пространстве разделяются на правые и левые. От выбора О. пространства зависит знак объёмов, ограниченных ориентированными поверхностями, смысл векторного произведения двух векторов и т.п.

В научной и учебной литературе употребляются как левая, так и правая системы пространственных координат. Например, в отечественных сочинениях по математике распространено употребление левой системы, в сочинениях же по механике и физике — правой системы.

Понятие «О.» распространяется также и на многомерные пространства .

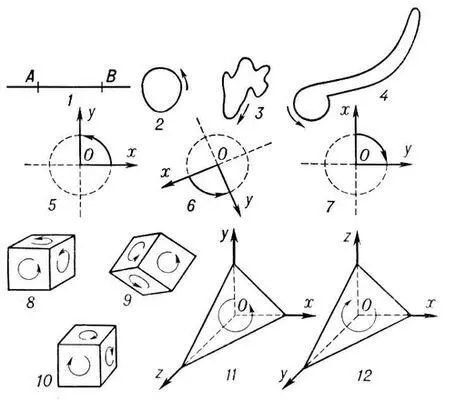
Рис. к ст. Ориентация.

Ориента'ция живо'тных,присущая животным способность определять своё положение в пространстве, среди особей того же или др. видов, т. е. в популяции и биоценозе . О. ж. — сложный процесс, включающий получение информации о внешнем мире по разным каналам связи (рецепторным системам), её обработку, сопоставление в центральной нервной системе и формирование ответной реакции. Приём и обработка сигналов состоят из распознавания образа (информационного содержания сигнала) и его локации — определения положения источника сигнала по отношению к организму, что осуществляется разными рецепторными системами ( биолокация ).

Оптическая О. ж. определяется прежде всего возможностями зрения органов : глаз и других светочувствительных рецепторов . Последние обычно способны лишь регистрировать степень освещённости, спектральный состав света и степень его поляризации. Так, у ланцетника, примитивного хордового животного, живущего в морском грунте, светочувствительные органы — глазки Гессе — расположены по всей длине прозрачного тела, вдоль нервной трубки; они регистрируют, всё ли тело животного погружено в грунт, т. е. защищено от нападения хищника. Образное зрение беспозвоночных и особенно позвоночных резко увеличивает возможности О. ж. в окружающей среде. Необходимость этого возрастает при увеличении подвижности животных. Детальность и сложность анализа зримого мира невелика у беспозвоночных и низших позвоночных. На общем фоне они выделяют лишь немногие биологически важные сигналы. Лягушки, например, «видят» лишь движущиеся предметы небольших размеров (мелких животных, служащих пищей) и реагируют на быстрое затенение («враг»); всё остальное воспринимается ими как безразличный фон. Детальность отражения резко возрастает у насекомых, а также у птиц и млекопитающих, способных ориентироваться не только по множеству «земных» ориентиров, но и по положению Солнца, Луны и звёзд (астронавигация). По ним ориентируются и мелкие раки, возвращающиеся при отливе в море. Рыжие лесные муравьи способны учитывать и положение Луны. «Инстинкт дома» — способность возвращаться на свой участок или в убежище даже из незнакомого места — объясняется запоминанием характерных особенностей ландшафта и астронавигацией. Обязательное условие астронавигации — наличие «биологических часов», т. е. способности организма ориентироваться во времени.