БСЭ БСЭ - Большая Советская Энциклопедия (ОС)

Кодификация законодательства 60—70-х гг., осуществляемая на базе Конституции СССР 1936, призвана привести советское законодательство в соответствие с потребностями современного этапа коммунистического строительства. Новые О. з. содержат в систематическом изложении определяющие положения соответствующих отраслей законодательства и наиболее важные нормы по вопросам, которые во всех республиках должны решаться одинаково. Каждая союзная республика воспроизводит в своём кодексе или законе положения и нормы О. з., дополняет их развивающими и конкретизирующими нормами, отражающими специфические условия хозяйства, быта, жизни республики.

В 1958—74 Верховный Совет СССР принял 12 законов типа О. з., принятию которых предшествовали глубокая научная подготовка и, как правило, всенародное обсуждение подготовленных законопроектов. На 1 июля 1974 действуют следующие О. з. Союза ССР и союзных республик: Основы земельного законодательства (приняты 13 декабря 1968, введены в действие с 1 июля 1969); Основы водного законодательства (приняты 10 декабря 1970, введены в действие с 1 сентября 1971); Основы законодательства о здравоохранении (приняты 19 декабря 1969, введены в действие с 1 июля 1970); Основы законодательства о народном образовании (приняты 19 июля 1973, введены в действие с 1 января 1974); Основы законодательства о труде (приняты 15 июля 1970, введены в действие с 1 января 1971); Основы законодательства о судоустройстве (приняты 25 декабря 1958); Основы гражданского законодательства (приняты 8 декабря 1961, введены в действие с 1 мая 1962); Основы законодательства о браке и семье (приняты 27 июня 1968, введены в действие с 1 октября 1968); Основы гражданского судопроизводства (приняты 8 декабря 1961, введены в действие с 1 мая 1962); Основы уголовного законодательства (приняты 25 декабря 1958); Основы уголовного судопроизводства (приняты 25 декабря 1958); Основы исправительно-трудового законодательства (приняты 11 июля 1969, введены в действие с 1 ноября 1969).

Лит.: Основы законодательства Союза ССР и союзных республик, М., 1971.

А. Ф. Шебанов.

Осоавиахи'м, Общество содействия обороне, авиационному и химическому строительству, массовая добровольная общественная организация граждан Советского Союза, существовавшая в 1927—48. Основными задачами О. являлись содействие укреплению обороноспособности страны, распространение военных знаний среди населения, воспитание его в духе советского патриотизма. В 1948 вместо О. были образованы 3 самостоятельных общества — ДОСАВ, ДОСАРМ и ДОСФЛОТ. В 1951 эти общества были объединены в ДОСААФ СССР.

Осо'бая ма'трица(матем.), квадратная матрица А = 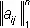порядка n , определитель которой равен нулю, т. е. ранг которой меньше n . Матрица является особой в том и только в том случае, когда между её строками (а также и между столбцами) существует линейная зависимость .

Осо'бая то'чкав математике.

1) Особая точка кривой, заданной уравнением F ( x, у ) = 0, — точка М 0( х 0, y 0 ), в которой обе частные производные функции F ( x, у ) обращаются в нуль:

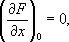
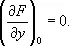
Если при этом не все вторые частные производные функции F ( x, у ) в точке М 0равны нулю, то О. т. называют двойной. Если наряду с обращением в нуль первых производных в точке М 0обращаются в нуль и все вторые производные, но не все третьи производные равны нулю, то О. т. называется тройной, и т.д. При исследовании строения кривой вблизи двойной О. т. важную роль играет знак выражения

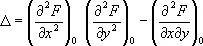
Если D > 0, то О. т. называется изолированной; например, у кривой у 2— х 4+ 4x 2 = 0 начало координат есть изолированная О. т. (см. рис. 1 ). Если D < 0, то О. т. называется узловой, или точкой самопересечения; например, у кривой ( x 2+ y 2+ a 2 ) 2— 4a 2x 2— a 4 = 0 начало координат есть узловая О. т. (см. рис. 2 ). Если D = 0, то О. т. кривой является либо изолированной, либо характеризуется тем, что различные ветви кривой имеют в этой точке общую касательную, например: а) точка возврата 1-го рода — различные ветви кривой расположены по разные стороны от общей касательной и образуют остриё, как у кривой у 2— х 3 = 0 (см. рис. 3, a ); б) точка возврата 2-го рода — различные ветви кривой расположены по одну сторону от общей касательной, как у кривой ( у — x 2 ) 2— х 5 = 0 (см. рис. 3 , б); в) точка самоприкосновения (для кривой у 2— х 4 = 0 начало координат является точкой самоприкосновения; (см. рис. 3 , в). Наряду с указанными О. т. имеется много других О. т. со специальными названиями; например, асимптотическая точка — вершина спирали с бесконечным числом витков (см. рис. 4 ), точка прекращения, угловая точка и т.д.

Лит. см. при ст. Дифференциальная геометрия .

2) Особая точка дифференциального уравнения — точка, в которой одновременно обращаются в нуль и числитель и знаменатель правой части дифференциального уравнения

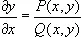, (1)

где Р и Q — непрерывно дифференцируемые функции. Предполагая О. т. расположенной в начале координат и используя Тейлора формулу , можно представить уравнение (1) в виде

,

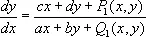где P 1( x, у ) и Q 1( x, у )— бесконечно малые по отношению к 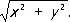Характер поведения интегральных кривых около О. т. зависит от корней l 1и l 2характеристического уравнения

.

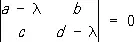Именно, если l 1¹ l 2и l 1l 2> 0 или l 1= l 2, то О. т. есть узел; все интегральные кривые, проходящие через точки достаточно малой окрестности узла, входят в него. Если l 1¹ l 2и l 1l 2< 0, то О. т. есть седло; в окрестности седла четыре интегральные кривые (сепаратрисы) входят в О. т., а между ними располагаются интегральные кривые типа гипербол. Если l 1,2= a ± i b, a ¹ 0 и b ¹ 0, то О. т. есть фокус; все интегральные кривые, проходящие через точки достаточно малой окрестности фокуса, представляют собой спирали с бесконечным числом витков в любой сколь угодно малой окрестности фокуса. Если, наконец, l 1,2= ± i b, b ¹ 0, то характер О. т. не определяется одними линейными членами в разложениях Р ( х, у ) и Q ( x, у ), как это имело место во всех перечисленных случаях; здесь О. т. может быть фокусом или центром, а может иметь и более сложный характер. В окрестности центра все интегральные кривые являются замкнутыми и содержат центр внутри себя. Так, например, точка (0, 0) является узлом для уравнений у ' = 2 у/х (l 1= 1, l 2= 2; см. рис. 5 , а) и y ' = у/х (l 1= l 2= 1; см. рис. 5 , б), седлом для уравнения у' = —у/х (l 1= —1, l 2= 1 ; см. рис. 6 ), фокусом для уравнения у' = ( х + у ) / ( х — у ) (l 1= 1 — i , l 2= 1 + i ; см. рис. 7 ) и центром для уравнения у' = —x / y (l 1= —i , l 2= i ; см. рис. 8 ).