БСЭ БСЭ - Большая Советская Энциклопедия (ОС)

Если , то О. т. называют особой точкой высшего порядка. О. т. высшего порядка могут принадлежать к указанным типам, но могут иметь и более сложный характер. В случае, когда функции Р ( х, у ) и Q ( х, у ) аналитические, окрестность О. т. высшего порядка может распадаться на области: D 1— заполненные интегральными кривыми, обоими концами входящими в О. т. (эллиптические области), D 2— заполненные интегральными кривыми, одним концом входящими в О. т. (параболические области), и D 3— области, ограниченные двумя интегральными кривыми, входящими в О. т., между которыми расположены интегральные кривые типа гипербол (гиперболические области) (см. рис. 9 ). Если нет интегральных кривых, входящих в О. т., то О. т. называется точкой устойчивого типа. Окрестность устойчивой О. т. состоит из замкнутых интегральных кривых, содержащих О. т. внутри себя, между которыми расположены спирали (см. рис. 10 ).

Изучение О. т. дифференциальных уравнений, т. е. по существу изучение поведения семейств интегральных кривых в окрестности О. т., составляет один из разделов качественной теории дифференциальных уравнений и играет важную роль в приложениях, в частности в вопросах устойчивости движения (работы А. М. Ляпунова , А. Пуанкаре и др.).

Лит. см. при ст. Дифференциальные уравнения .

3) Особая точка однозначной аналитической функции — точка, в которой нарушается аналитичность функции (см. Аналитические функции ). Если существует окрестность О. т. a , свободная от других О. т., то точку а называют изолированной О. т. Если а — изолированная О. т. и существует конечный 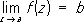, то a называют устранимой О. т. Путём надлежащего изменения определения функции в точке а (или доопределения её в этой точке, если функция в ней вообще не определена), именно, полагая f ( a ) = b , можно добиться того, что a станет обыкновенной точкой исправленной функции. Например, точка z = 0 является устранимой О. т. для функции 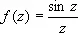, так как 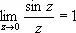; для функции f 1( z ) = f ( z ), если z ¹ 0, и f 1(0), = 1, точка z = 0 является обыкновенной точкой [ f 1( z ) аналитична в точке z = 0]. Если а — изолированная О. т. и 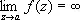, то а называют полюсом или несущественно особой точкой функции f ( z ), если же 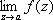не существует, то существенно особой точкой. Ряд Лорана (см. Лорана ряд ) функции f ( z ) в окрестности изолированной О. т. не содержит отрицательных степеней z — а , если а — устранимая О. т., содержит конечное число отрицательных степеней z — а , если а — полюс (при этом порядок полюса р определяется как наивысшая степень 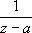, встречающаяся в ряде Лорана), и содержит как угодно высокие степени 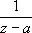, если а — существенно особая точка. Например, для функции

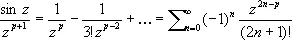( p = 2, 3, …)

точка z = 0 является полюсом порядка р , для функции

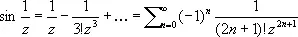
точка z = 0 является существенно особой точкой.

На границе круга сходимости степенного ряда должна находиться по крайней мере одна О. т. функции, представляемой внутри этого круга данным степенным рядом. Все граничные точки области существования однозначной аналитической функции (естественной границы) являются О. т. этой функции. Так, все точки единичного круга | z | = 1 являются особыми для функции

.

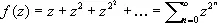Для многозначной аналитической функции понятие «О. т.» более сложно. Помимо О. т., в отдельных листах римановой поверхности функции (то есть О. т. однозначных аналитических элементов) всякая точка ветвления также является О. т. функции. Изолированные точки ветвления римановой поверхности (то есть такие точки ветвления, что в некоторой их окрестности ни в одном листе нет других О. т. функции) классифицируются следующим образом. Если а — изолированная точка ветвления конечного порядка и существует конечный 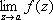, то О. т. называют обыкновенной критической точкой; если же 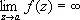, то а называют критическим полюсом. Если а — изолированная точка ветвления бесконечного порядка и 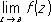существует (конечный или бесконечный), то а называют трансцендентной О. т. Все остальные изолированные точки ветвления называют критическими существенно особыми точками. Примеры: точка z = 0 является обыкновенной критической точкой функции 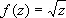, критическим полюсом функции 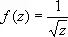, трансцендентной О. т. функции f ( z ) = ln z и критической существенно особой точкой функции f ( z ) = sin ln z .

Всякая О. т., кроме устранимой, является препятствием при аналитическом продолжении, т. е. аналитическое продолжение вдоль кривой, проходящей через неустранимую О. т., невозможно.

Лит. см. при ст. Аналитические функции .

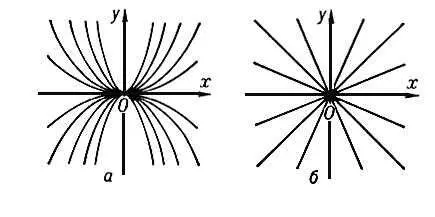
Рис. 5 к ст. Особая точка.

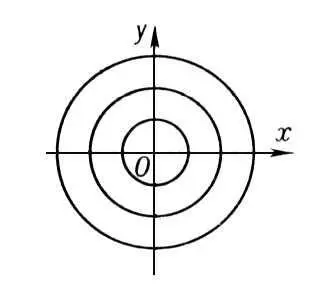
Рис. 8 к ст. Особая точка.

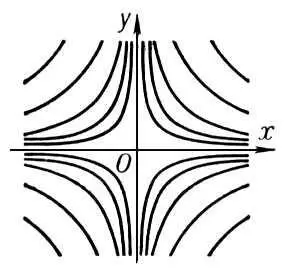
Рис. 6 к ст. Особая точка.

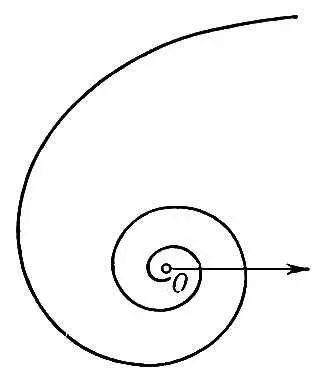
Рис. 4 к ст. Особая точка.

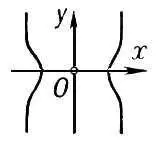
Рис. 1 к ст. Особая точка.

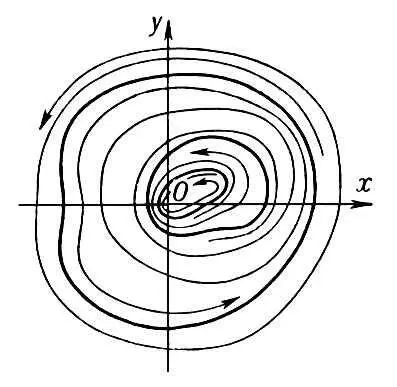
Рис. 10 к ст. Особая точка.