БСЭ БСЭ - Большая Советская Энциклопедия (ОТ)

Из принципа относительности вытекает, что физические законы должны иметь одинаковую форму во всех и. с. о.; следовательно, они должны сохранять свой вид при преобразованиях Лоренца. Это требование называется принципом (постулатом) релятивистской инвариантности, или лоренц-инвариантности (лоренц-ковариантности), законов природы.

Из преобразований Лоренца вытекает релятивистский закон сложения скоростей. Если частица или сигнал движется в L по оси х со скоростью u , то в момент tx = ut и скорость частицы u’ = x’ / t’ , измеряемая в системе L’ , равна:

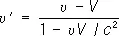(3)

Эта формула отражает основную черту релятивистской кинематики — независимость скорости света от движения источника. Действительно, если скорость света, испущенного покоящимся в некоторой и. с. о. L источником, есть с , u = с , то из закона сложения скоростей (2) получаем, что измеренная в и. с. о. L’ скорость света u’ также равна с . Так как направление оси х произвольно, то отсюда следует независимость скорости света от движения источника. Это свойство скорости света однозначно определяет вид преобразований Лоренца: постулировав независимость скорости света от движения источника, однородность пространства и времени и изотропию пространства, можно вывести преобразования Лоренца.

Особая роль скорости света в О. т. связана с тем, что она является предельной скоростью распространения сигналов и движения частиц, достигаемой при энергии частицы, стремящейся к бесконечности, или массе, стремящейся к нулю; если бы масса покоя m gфотона оказалась хотя и очень малой, но отличной от нуля (экспериментально установлено, что m g < 4×10 –21 m e, где m e — масса электрона), то скорость света была бы меньше предельной. Чтобы предельная скорость вообще могла существовать, она не должна зависеть от движения источника частиц.

Из преобразований Лоренца легко получить основные эффекты О. т.: относительность одновременности, замедление времени, сокращение продольных размеров движущихся тел. Действительно, события 1, 2, одновременные в одной и. с. о. L : t 1= t 2и происходящие в разных точках x 1, x 2, оказываются неодновременными в другой и. с. о. L’ : 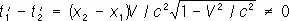. Далее, когда часы, покоящиеся в L в точке х = 0, показывают время t , то время t’ по часам в L’ , пространственно совпадающим с часами в L в этот момент времени, есть

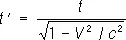(4)

или

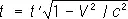(4, а)

т. е. с точки зрения наблюдателя в L’ часы в L отстают. В силу принципа относительности отсюда следует, что с точки зрения наблюдателя в L’ , все процессы в L замедлены в такое же число раз.

Легко получить также, что размеры l всех тел, покоящихся в L , оказываются при измерении в L’ сокращёнными в 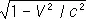раз в направлении V :

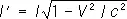(5)

В частности, продольный диаметр сферы, движущейся со скоростью u относительно L’ , будет при измерении в L ¢ в 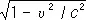раз короче, чем поперечный. (Заметим, что это сокращение не обнаружилось бы на мгновенной фотографии сферы: из-за различного запаздывания световых сигналов, приходящих от разных точек сферы, её видимая форма остаётся прежней.)

Для и. с. о. пространственно-временные эффекты, определяемые преобразованиями Лоренца, относительны: с точки зрения наблюдателя в L замедляются все процессы и сокращаются все продольные масштабы в L’ . Однако это утверждение несправедливо, если хотя бы одна из систем отсчёта неинерциальна. Если, например, часы 1 перемещаются относительно L из А в В со скоростью u , а потом из В в А со скоростью — u , то они отстанут по сравнению с покоящимися A часами 2 в 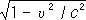раз; это можно обнаружить прямым сравнением, так что эффект абсолютен. Он должен иметь место для любого процесса; например, близнец, совершивший путешествие со скоростью u , вернётся в 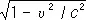раз более молодым, чем его брат, остававшийся неподвижным в и. с. о. Это явление, получившее название «парадокса близнецов», в действительности не содержит парадокса: система отсчёта, связанная с часами 1, не является инерциальной, т.к. эти часы при повороте в В испытывают ускорение по отношению к инерциальной системе; поэтому часы 1 и 2 неравноправны.

При малых скоростях u преобразования Лоренца переходят в преобразования Галилея x’ = x – ut , y ’ = y , z’ ’ = z , t ’ = t , которые описывают связь между картинами различных наблюдателей, известную из повседневного опыта: размеры предметов и длительность процессов одинаковы для всех наблюдателей.

Преобразования Пуанкаре оставляют инвариантной величину, называемую интервалом s AB между событиями А , В , которая определяется соотношением:

s 2 AB = c 2( t A – t B ) 2– ( x A – x B ) 2– ( y A – y B ) 2– ( z A – z B ) 2. (6)

Математически инвариантность s аналогична инвариантности расстояния при преобразованиях движения в евклидовой геометрии. Величины ct , х , у , z можно рассматривать как четыре координаты события в четырёхмерном пространстве Минковского: х 0= ct , х 1= х , x 2= у , x 3= z , которые являются компонентами четырёхмерного вектора.

Если вместо x 0ввести мнимую координату x 4= ix 0= ict , то произвольное преобразование Пуанкаре можно записать в виде, полностью аналогичном формуле, описывающей вращения и сдвиги в трёхмерном пространстве.

Вследствие того, что квадраты разностей временны'х и пространственных координат входят в (6) с разными знаками, знак s 2может быть различным; геометрия такого пространства отличается от евклидовой и называется псевдоевклидовой. В такой геометрии интервалы разделяются на три типа: s 2< 0, s 2> О и s 2= 0. Интервалы первого и второго типа называются соответственно времениподобными и пространственноподобными. Если s 2³ 0, знак t A – t B не зависит от системы отсчёта. Это тесно связано с принципом причинности. Действительно, если s 2³ 0 и (для определённости) t A< t B , то события А и В могут быть связаны сигналом, распространяющимся со скоростью u £ с , т.е. А может быть причиной В . Обычные представления о причинности требуют тогда, чтобы в любой системе отсчёта событие В следовало за событием А . Инвариантность условия s 2= 0 непосредственно выражает инвариантность скорости света. Если s 2< 0, то знак t A – t B может быть различным в разных и. с. о. Однако это не противоречит причинности, т.к. такие события не могут быть связаны никаким взаимодействием.