БСЭ БСЭ - Большая Советская Энциклопедия (ОТ)

Если s 2< 0, то существует такая система отсчёта, в которой события А и В одновременны; в этой системе s 2= – l 2, где l — обычное расстояние. При s 2> 0 существует система отсчёта, в которой события А и В происходят в одной точке.

В классической физике требование инвариантности законов физики относительно преобразований Лоренца означает, что любые физические величины должны преобразовываться как скаляры , векторы или тензоры в пространстве Минковского. Правила вычислений с такими величинами даются тензорным исчислением. Использование тензорного исчисления позволяет записывать законы физики в таком виде, что их лоренц-инвариантность становится непосредственно очевидной.

Законы сохранения в теории относительности и релятивистская механика

В О. т., так же как в классической механике, для замкнутой физической системы сохраняется импульс р и энергия Е . Трёхмерный вектор импульса вместе с энергией образует четырёхмерный вектор импульса-энергии с компонентами Е / с , р , обозначаемый как ( Е / с , р ). При преобразованиях Лоренца остаётся инвариантной величина

E 2 – (cp) 2 = m 2 c 4 , (7)

где m – масса покоя частицы. Из требований лоренц-инвариантности следует, что зависимость энергии и импульса от скорости имеет вид

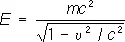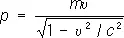, . (8)

Энергия и импульс частицы связаны соотношением р = Eu / c 2. Это соотношение справедливо также для частицы с нулевой массой покоя; тогда u = с и р = Е/с. Такими частицами, по-видимому, являются фотоны (g) и электронные и мюонные нейтрино. Из (8) видно, что импульс и энергия частицы с m ¹ 0 стремятся к бесконечности при u ® с .

Обсуждалась возможность существования объектов, движущихся со скоростью, большей скорости света (т. н. тахионов). Формально это не противоречит лоренц-инвариантности, но приводит к серьёзным затруднениям с выполнением требования причинности.

Масса покоя т не является сохраняющейся величиной. В частности, в процессах распадов и превращений элементарных частиц сумма энергий и импульсов частиц сохраняется, а сумма масс покоя меняется. Так, в процессе аннигиляции позитрона и электрона е ++ е –® 2g сумма масс покоя изменяется на 2 m е.

В системе отсчёта, в которой тело покоится (такая система отсчёта наз. собственной), его энергия (энергия покоя) есть Е 0= mс 2. Если тело, оставаясь в покое, изменяет своё состояние, получая энергию в виде излучения или тепла, то из релятивистского закона сохранения энергии следует, что полученная телом энергия D Е связана с увеличением его массы покоя соотношением D Е = D mc 2. Из этого соотношения, названного Эйнштейном принципом эквивалентности массы и энергии, следует, что величина Е 0= mc 2 определяет максимальную величину энергии, которая может быть «извлечена» из данного тела в системе отсчёта, в которой оно покоится.

Для движущегося тела величина

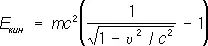(9)

определяет его кинетическую энергию. При u << с (9) переходит в нерелятивистское выражение Е кин= mu 2/2, при этом импульс равен р = mu . Из определения Е кинследует, что для любого процесса в изолированной системе выполняется равенство:

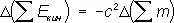, (10)

согласно которому увеличение кинетической энергии пропорционально уменьшению суммы масс покоя. Это соотношение широко используется в ядерной физике; оно позволяет предсказывать энерговыделение в ядерных реакциях, если известны массы покоя участвующих в них частиц. Возможность протекания процессов, в которых происходит превращение энергии покоя в кинетическую энергию частиц, ограничена др. законами сохранения (например, законом сохранения барионного заряда , запрещающим процесс превращения протона в позитрон и g-квант).

Иногда вводят массу, определяемую как

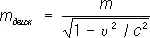; (11)

при этом связь между импульсом и энергией имеет тот же вид, что и в ньютоновской механике: р = m движ u . Определённая таким образом масса отличается от энергии тела лишь множителем 1/ с 2. (В теоретич. физике часто выбирают единицы измерения так, что с = 1, тогда Е = m движ.)

Основные уравнения релятивистской механики имеют такой же вид, как второй закон Ньютона и уравнение энергии, только вместо нерелятивистских выражений для энергии и импульса используются выражения (8):

,

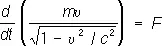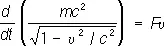, (12)

где F — сила, действующая на тело. Для заряженной частицы, движущейся в электромагнитном поле, F есть Лоренца сила .

Теория относительности и эксперимент

Предположения о точечных событиях, справедливости принципа относительности, однородности времени и однородности и изотропии пространства с неизбежностью приводят к О. т. При этом абстрактно допустим предельный случай, соответствующий с = ¥, однако такая возможность исключена экспериментально: доказано с огромной точностью (см. ниже), что предельная скорость с есть скорость света в вакууме (её значение дано в начале статьи).

Каковы границы применимости О. т.? Отклонения от пространственно-временной геометрии О. т., связанные с гравитацией, наблюдаемы и рассчитываются в ОТО; никаких др. ограничений применимости О. т. пока не обнаружено, хотя неоднократно высказывались подозрения, что на очень малых расстояниях (например, ~10 –17 см ) понятие точечного события, а следовательно, и О. т. могут оказаться неприменимыми (см., например, Квантование пространства-времени ).

Предположение о лоренц-инвариантности и точечности событий (означающей локальность взаимодействий) лежит в основе всех современных теорий, в которых существен релятивизм. Справедливость квантовой электродинамики электронов и мюонов , а следовательно, и О. т. установлена вплоть до расстояний 10 –15 см . При энергиях порядка масс этих частиц согласие квантовой электродинамики с опытом установлено с относительной точностью, несколько лучшей, чем 10 –5; с точностью того же порядка должна быть справедлива и механика О. т.