БСЭ БСЭ - Большая Советская Энциклопедия (ПЕ)

Лит.: Каплан А. В., Закрытые повреждения костей и суставов, 2 изд., М., 1967; Уотсон-Джонс Р., Переломы костей и повреждения суставов, пер. с англ., М., 1972.

В. Ф. Пожариский.

Перемагни'чивание,изменение направления намагниченности ферро- или ферримагнитного образца на противоположное под действием внешнего магнитного поля (подробнее см. Гистерезис, Намагничивание ).

Переме'нная,переменное, одно из основных понятий математики и логики. Начиная с работ П. Ферма, Р. Декарта, И. Ньютона, Г. В. Лейбница и др. основоположников «высшей» математики под П. понимали некоторую «величину», которая может «изменяться», принимая в процессе этого изменения различные «значения». Тем самым П. противопоставлялись «постоянным» (или константам) — числам или каким-либо др. «величинам», каждая из которых имеет единственное, вполне определённое значение (см. Переменные и постоянные величины ) . По мере развития математики и в ходе её обоснования представления о «процессах», «изменении величин» и т. п. тщательно изгонялись из математического арсенала как «внематематические», в результате чего П. стала пониматься как обозначение для произвольного элемента рассматриваемой предметной области (например, области натуральных чисел или действительных чисел), то есть как родовое имя всей этой области (в отличие от констант — «собственных имён» для чисел или др. конкретных предметов рассматриваемой области). Этот пересмотр взглядов на понятие П. был тесно связан с перестройкой математики на базе множеств теории, завершившейся в конце 19 в. При всей простоте и «естественности» такой перестройки она существенным образом опирается на так называемую абстракцию актуальной бесконечности, позволяющую рассматривать произвольные бесконечные множества в качестве «данных» («завершенных», «готовых», «актуальных») объектов и применять по отношению к ним любые средства классической логики, отвлекаясь от незавершённости и принципиальной незавершимости процесса образования такого множества. Трудности решения логических проблем, связанных с принятием этой абстракции, делают понятной частичную «реабилитацию» старинных представлений о «переменных величинах»; при построении математических теорий представители некоторых школ (см. Математический интуиционизм, Конструктивное направление ) предпочитают обходиться боле (слабой, но зато менее уязвимой в логическом отношении абстракцией потенциальной осуществимости, с точки зрения которой с бесконечными множествами как раз связываются представления о процессах их «порождения»,— сколь угодно далеко заходящих, но никогда не завершающихся (см. Бесконечность в математике). При исследовании вопроса непротиворечивости различных областей математики на такую позицию фактически встаёт значительное большинство математиков и логиков (см. Метаматематика ) .

В формализованных языках ( исчислениях, формальных системах) математической логики П. называются символы строго фиксированного вида, могущие при определённых условиях заменяться выражениям данного исчисления. Это относится к так называемым свободным (или значащим) П. примером которых может служить П. в неравенстве х > 5, обращающемся при подстановке вместо х, скажем, цифры 7 (то есть обозначения для числа) 7 в истинное высказывание, а при подстановке цифры 2 — в ложное высказывание. Что касается так называемых связанных (или фиктивных) П., то они сами по себе вообще ничего не означают, несут чисто синтаксические функции и могут (при соблюдении некоторых элементарных предосторожностей) «переименовываться», то есть заменяться др. П. Такова, например, П. у в записях 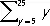или " yP (y) , в интерпретации (прочтения) которых она вообще не входит и может быть заменена любой др. П. так, первая из них (читаемая как «сумма целых чисел от 5 до 25») может быть заменена на 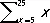или 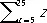, а вторая («все числа обладают свойством Р») на " tP (t). Различают индивидные, пропозициональные, предикатные, функциональные, числовые и др. виды П., вместо которых можно (согласно специальным правилам подстановки) подставлять соответственно обозначения предметов из рассматриваемой области («термы»), обозначения для конкретных высказываний, предикатов, функций, чисел и др. Т. о., П. можно содержательно понимать как «пустое место» в формуле, снабженное указанием, чем это «место» может быть «заполнено» (своего рода «тара под строго определенный товар»).

Свободные вхождения П. в выражения содержательных научных теорий и формулы логико-математических исчислений (соответствующие употреблению неопределенных местоимений в обычной речи) допускают различные интерпретации. Первая (соответствующая применению всякого рода процедур подстановок) — так называемая предикатная интерпретация: формула A ( x 1,..., x n ) какого-либо исчисления понимается как некоторый местный предикат. Та же формула может интерпретироваться и как предложение ( высказывание ) , а именно как предложение " x 1… " x n A ( x 1… x n ), являющееся ее «замыканием»,— это так называемая интерпретация всеобщности (употребительная, например, при формулировке аксиом различных научных теорий). Свободным П. могут, наконец, приписываться значения, постоянные в пределах некоторого контекста (например, вывода из данной совокупности формул), их тогда называют параметрами этого контекста и говорят об их условной интерпретации. Например, П. х в выражении cos х, взятом изолированно, имеет предикатную интерпретацию, в тождестве sin 2 x + cos 2x = 1 — интерпретацию всеобщности, в уравнении cos х = 1 (в процессе его решения, когда эта П. именуется «неизвестным») — условную интерпретацию.

Таким образом, на различных уровнях формализации понятие П. выступает как уточнение средств, общеупотребительных в обычных разговорных языках (неопределенные местоимения, неопределенные артикли), и различных способов использования этих средств.

См. также Квантор, Логика предикатов, Математика.

Лит.: Клини С. К, Введение в метаматематику, пер с англ, М., 1957, §§ 31, 32, 45, Чёрч А, Введение в математическую логику, пер с англ, т. 1, М., 1960, §§ 02, 04, 06.

Переме'нного то'ка генера'тор,машина, преобразующая механическую энергию вращения в электрическую энергию переменного тока. Различают синхронные и асинхронные П, т. г. Асинхронные генераторы, имевшие ограниченное применение, главным образом в автономных системах электропитания, к 70-м гг. 20 в. практически полностью заменены синхронными генераторами. Наибольшее применение имеют трехфазные П. т. г.; однофазные П. т. г. не получили распространения, так как их характеристики и эксплуатационные качества значительно хуже, чем у трехфазных. Мощные П. т. г. устанавливают на электростанциях (см. Турбогенератор, Гидрогенератор ) ; П. т. г. относительно небольшой мощности работают в системах автономного энергоснабжения (см. Дизельная электростанция, Газотурбинная электростанция ) и в преобразователях частоты (см. Двигатель-генераторный агрегат ) .