БСЭ БСЭ - Большая Советская Энциклопедия (ПЕ)

III. Теоретические исследования переменных звёзд

Причины изменений блеска физических П. з. и место, занимаемое этими звёздами в звёздной эволюции, составляют тесно связанный круг проблем. По-видимому, переменность характерна для звёзд на определённых этапах их эволюции. Особое значение для понимания природы переменности имеет изучение П. з. в звёздных скоплениях (для звёзд, входящих в скопления, можно определить и возраст, и эволюционную стадию), а также анализ положения П. з. разных типов на диаграмме «спектр — светимость» (см. Герцшпрунга — Ресселла диаграмма ) .

Скопления, содержащие быстрые неправильные П. з., очень молоды (их возраст 10 6—10 7лет). В этих скоплениях лишь наиболее массивные звёзды, обладающие значительной светимостью, достигли главной последовательности на диаграмме Герцшпрунга — Ресселла, занимают её верхнюю часть и являются обычными стационарными звёздами. У звёзд меньшей светимости и массы ещё не закончилось гравитационное сжатие, сохранилась обширная конвективная зона, в которой происходят неправильные бурные движения газа, с этим, по-видимому, и связана переменность блеска и спектра молодых звёзд.

Ряд типов пульсирующих П. з. расположен на диаграмме Герцшпрунга — Ресселла в пределах полосы нестабильности, пересекающей диаграмму от красных сверхгигантов спектрального класса К до белых звёзд-карликов класса А. К их числу принадлежат цефеиды, звёзды типа RV Тельца, RR Лиры и d Щита. Во всех этих звёздах действует, по-видимому, единый механизм переменности, вызывающий пульсацию их верхних слоев. Звёзды, соседствующие на диаграмме Герцшпрунга — Ресселла, обладают схожими характеристиками переменности (например, цефеиды плоской и сферической составляющей), но их эволюционная история, массы, внутреннее строение резко отличаются.

Изучение пространственно-кинематических характеристик П. з. было одним из главных факторов, приведших в 40-х гг. 20 в. к разработке концепции составляющих Галактики и звёздных населений (см. Галактика ) .

Лит.: Общий каталог переменных звезд, 3 изд., т. 1—3, М., 1969—71; Пульсирующие звезды, М., 1970; Эруптивные звезды, М., 1970; Затменные переменные звезды, М., 1971; Методы исследования переменных звезд, М., 1971.

Ю. Н. Ефремов.

Переме'нные и постоя'нные величи'ны,величины, которые в изучаемом вопросе принимают различные значения либо, соответственно, сохраняют одно и то же значение. Например, при изучении падения тела расстояние последнего от земли и скорость падения — переменные величины, ускорение же (если пренебречь сопротивлением воздуха) — величина постоянная. Элементарная математика рассматривала все изучаемые ею величины как постоянные. Понятие переменной величины возникло в математике в 17 в. под влиянием запросов естествознания, выдвинувшего на первый план изучение движения — процессов, а не только состояний. Это понятие не укладывалось в формы, выработанные математикой древности и средних веков, и требовало для своего выражения новых форм. Такими новыми формами явились буквенная алгебра и аналитическая геометрия Р. Декарта. В буквах декартовой алгебры, могущих принимать произвольные числовые значения, и нашли своё символическое выражение переменные величины. «Поворотным пунктом в математике была Декартова переменная величина. Благодаря этому в математику вошли движение и тем самым диалектика и благодаря этому же стало немедленно необходимым дифференциальное и интегральное исчисление...» (Энгельс Ф., см. Маркс К. и Энгельс Ф., Соч., 2 изд., т. 20, с. 573). В этот период и вплоть до середины 19 в. преобладают механические воззрения на переменные величины. Наиболее ярко они были выражены И. Ньютоном, называвшим переменные величины «флюэнтами», то есть текущими, и рассматривавшим их «... не как состоящие из крайне малых частей, но как описываемые непрерывным движением» («Математические работы», М., 1937, с. 167). Эти воззрения оказались весьма плодотворными и, в частности, позволили Ньютону совершенно по-новому подойти к нахождению площадей криволинейных фигур. Ньютон впервые стал рассматривать площадь криволинейной трапеции ( ABNM на рис. ) не как постоянную величину (вычисляемую суммированием составляющих её бесконечно малых частей), а как переменную величину, производимую движением ординаты кривой ( NM ) ; установив, что скорость изменения рассматриваемой площади пропорциональна ординате NM, он тем самым свёл задачу вычисления площадей к задаче определения переменной величины по известной скорости её изменения. Законность внесения в математику понятия скорости была обоснована в начале 19 в. теорией пределов, давшей точное определение скорости как производной. Однако в течение 19 в. постепенно выясняется ограниченность описанного выше воззрения на переменные величины. Математический анализ всё больше становится общей теорией функций, развитие которой невозможно без точного анализа сущности и объёма её основных понятий. При этом оказывается, что уже понятие непрерывной функции в действительности значительно сложнее, чем приведшие к нему наглядные представления. Открываются непрерывные функции, не имеющие производной ни в одной точке; понимать такую функцию как результат движения означало бы допускать движение, не имеющее скорости ни в какой момент. Всё большее значение приобретает изучение разрывных функций, а также функций, заданных на множествах значительно более сложной структуры, чем интервал или объединение нескольких интервалов. Ньютоновское толкование переменной величины становится недостаточным, а во многих случаях и бесполезным.

С другой стороны, математика начинает рассматривать как переменные не только величины, но и всё более разнообразные и широкие классы других своих объектов. На этой почве во 2-й половине 19 в. и в 20 в. развиваются теория множеств, топология и математическая логика. О том, насколько расширилось в 20 в. понятие переменной величины, свидетельствует тот факт, что в математической логике рассматриваются не только переменные, пробегающие произвольные множества предметов, но и переменные, значениями которых служат высказывания, предикаты (отношения между предметами) и т.д. (см. Переменная ) .

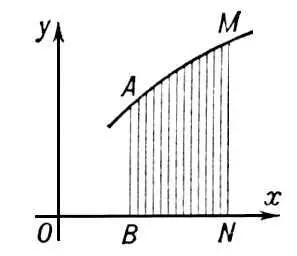
Рис. к ст. Переменные и постоянные величины.

Переме'нный лад,лад, в котором функция устоя (тоники) переходит от одного тона к другому (того же звукоряда), а также лад, звукоряд которого изменяется при одной и той же тонике (устое) (по И. В. Способину).