БСЭ БСЭ - Большая Советская Энциклопедия (ПО)

Показа'тель надёжноститехнического устройства, количественная характеристика его надёжности. В зависимости от того, сколько свойств характеризует П. н., он может быть единичным или комплексным. Единичный П. н. соответствует одному из свойств, такова интенсивность отказов. Комплексный П. н. соответствует нескольким свойствам, таков готовности коэффициент. П. н. неремонтируемых устройств являются численные характеристики случайной продолжительности их работы до отказа. П. н. ремонтируемых устройств служат характеристики соответствующих случайных потоков отказов. Наиболее часто используемые на практике показатели: средняя наработка до первого отказа, вероятность безотказной работы в заданном интервале времени, наработка на отказ, среднее значение параметра потока отказов, коэффициента готовности, коэффициента технического использования.

Лит.: Мартынов Г. К., Фомин В. Н., Показатели надёжности технических устройств, М., 1969.

Показа'тель преломле'ния, см. Преломления показатель.

Пока'затель тепла'в астрономии, разность визуальной и радиометрических звёздных величин небесного светила.

Подобно показателю цвета, характеризует распределение энергии в спектре объекта. Нульпункт системы П. т. установлен так, что П. т. равен нулю у звёзд спектрального класса АО. Радиометрические наблюдения производятся с помощью приёмников, регистрирующих всю попадающую на них энергию, — болометров, термоэлементов и радиометров. П. т. использовались при определении температуры звёзд. Понятие П. т. введено в 20-х гг. 20 в

Показа'тель цве'тав астрономии, разность звёздных величин, полученных в двух интервалах длин волн; характеризует основные черты распределения энергии в спектре небесного объекта, его цвет. Понятие П. ц. введено К. Шварцшильдом в начале 20 в. До 50-х гг. 20 в. основным являлся интернациональный П. ц., представляющий собой разность интернациональных фотографической и фотовизуальной звёздных величин. В современной астрономии в наиболее распространённой фотометрической системе UBV обычно используются П. ц. U—B и В—V, соответствующие разностям звёздных величин в ультрафиолетовой (U), синей (В) и жёлтой (V) частях спектра (см. Звёздная величина ) . Расширение системы UBV в красную и инфракрасную области (величины R, I и др.) позволяет получить другие П. ц., например V—R, V—I и т.п. Нульпункт П. ц. установлен так, чтобы все П. ц. равнялись бы нулю для ряда избранных близких звёзд-карликов спектрального класса А0. П. ц. В—V и U—B отрицательны для звёзд более ранних спектральных классов (более «голубых»), чем А0, и положительны для более поздних (более «красных»). В др. фотометрических системах нульпункты П. ц. могут отличаться от указанного. П. ц. определяются либо фотографически, либо фотоэлектрически. Используются при изучении межзвёздного поглощения света, природы и эволюции звёзд и звёздных систем и др. объектов.

Лит. см. при ст. Звёздная величина.

А. С. Шаров.

Показа'тельная фу'нкция, экспоненциальная функция, важная элементарная функция

f ( z ) = e z,

обозначается иногда exp z ; встречается в многочисленных приложениях математики к естествознанию и технике. Для любого значения z (действительного или комплексного) П. ф. определяется соотношением

;

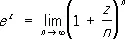Очевидно, что e 0 = 1; при n = 1 значение П. ф. равно е — основанию натуральных логарифмов. П. ф. обладает следующими основными свойствами:

и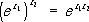

при любых значениях z 1 и z 2 , кроме того, на действительной оси ( рис. ) П. ф. e x > 0 и при n ® ¥ возрастает быстрее любой степени х, а при х ® - ¥ убывает быстрее любой степени 1/ x:

, ,

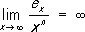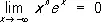каков бы ни был показатель n. Функцией, обратной по отношению к П. ф., является логарифмическая функция: если w = e z, то z = ln w .

Рассматривается также П. ф. a z при основаниях а > 0 , отличных от е [например, в школьном курсе математики для действительных значений z = х рассматриваются П. ф. 2 x, ( 1/ 2) x и т.д.]. П. ф. a z связана с П. ф. e z (основной) соотношением

a z= e zlna.

П. ф. e x является целой трансцендентной функцией. Она допускает следующее разложение в степенной ряд:

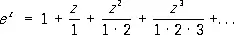, (1)

сходящийся во всей плоскости z. Равенство (1) также может служить определением П. ф.

Полагая z = х + iy, Л. Эйлер получил (1748) формулу:

e z = e x+iy= e x (cos y + i sin y ), (2)

связывающую П. ф. с тригонометрическими функциями. Из неё вытекают соотношения:

, .

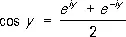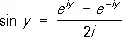Функции

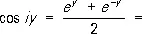ch y , 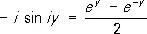= sh y

называются гиперболическими функциями, обладают рядом свойств, сходных со свойствами тригонометрических функций, и играют наряду с последними важную роль в различных приложениях математики.

Из соотношения (2) следует, что П. ф. (комплексного переменного z ) имеет период 2p i, то есть e z+2 pi = e z или e 2 p i = 1. Производная П. ф. равна самой функции: ( e z ) ' = e z.

Указанными свойствами П. ф. определяются её многочисленные приложения. В частности, П. ф. выражает закон (т. н. закон естественного роста), определяющий течение процессов, скорость которых пропорциональна наличному значению изменяющейся величины; примером могут служить химические мономолекулярные реакции или, при известных условиях, рост колоний бактерий. Периодичность П. ф. комплексного переменного наряду с другими её свойствами является причиной, по которой эта функция играет исключительно важную роль при изучении всяких периодических процессов, в частности колебаний и распространения волн.