БСЭ БСЭ - Большая Советская Энциклопедия (ПО)

И. С. Полбин.

По'лдень, момент, когда для данного места на Земле центр Солнца (истинного или т. н. среднего) находится в верхней кульминации. Прохождению через меридиан истинного Солнца соответствует истинный П., прохождению среднего Солнца — средний П. (см. Время ) . Время наступления П. зависит от географической долготы места: через каждые 15° к З. полдень наступает на 1 час позднее.

Полдневи'ца, посёлок городского типа в Поназыревском районе Костромской области РСФСР, в 32 км от ж.-д. станции Супротивный (на линии Буй — Котельнич). Шортюгский леспромхоз.

По'леалгебраическое, важное алгебраическое понятие, часто используемое как в самой алгебре, так и в др. отделах математики и являющееся предметом самостоятельного изучения.

Над обычными числами можно производить четыре арифметических действия (основные — сложение и умножение, и обратные им — вычитание и деление). Этим же характеризуются и П. Полем называется всякая совокупность (или множество) элементов, над которыми можно производить два действия — сложение и умножение, подчиняющиеся обычным законам (аксиомам) арифметики:

I. Сложение и умножение коммутативны и ассоциативны, т. е. a + b = b + a, ab = ba, a + ( b + c ) = ( a + b ) + c, a ( bc ) = ( ab ) c.

II. Существует элемент 0 (нуль), для которого всегда а + 0 = а; для каждого элемента а существует противоположный - а, и их сумма равна нулю. Отсюда следует, что в П. выполнима операция вычитания а - b.

III. Существует элемент е (единица), для которого всегда ае = а; для каждого отличного от нуля элемента а существует обратный a -1; их произведение равно единице. Отсюда следует возможность деления на всякое не равное нулю число а.

IV. Связь между операциями сложения и умножения даётся дистрибутивным законом: a ( b + c ) = ab + ac.

Приведём несколько примеров П.:

1) Совокупность Р всех рациональных чисел.

2) Совокупность R всех действительных чисел.

3) Совокупность К всех комплексных чисел.

4) Множество всех рациональных функций от одного или от нескольких переменных, например с действительными коэффициентами.

5) Множество всех чисел вида а + b 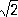, где а и b — рациональные числа.

6) Выбрав простое число р, разобьем целые числа на классы, объединив в один класс все числа, дающие при делении на р один и тот же остаток. Возьмём в двух классах по представителю и сложим их; тот класс, в который попадёт эта сумма, назовем суммой выбранных классов. Аналогично определяется произведение. При таком определении сложения и умножения все классы образуют П.; оно состоит из р элементов.

Из аксиом I, II следует, что элементы П. образуют коммутативную группу относительно сложения, а из аксиом I, III — то, что все отличные от 0 элементы П. образуют коммутативную группу относительно умножения.

Может оказаться, что в П. равно нулю целое кратное na какого-либо отличного от нуля элемента а. В этом случае существует такое простое число р, что р -кратное pa любого элемента а этого П. равно нулю. Говорят, что в этом случае характеристика П. равна р (пример 6). Если na ¹ 0 ни для каких отличных от нуля n и а, то считают характеристику П. равной нулю (примеры 1—5).

Если часть F элементов поля G сама образует П. относительно тех же операций сложения и умножения, то F называется подполем поля G, а G — надполем, или расширением поля F. П., не имеющее подполей, называется простым. Все простые П. исчерпываются П. примеров 1 и 6 (при всевозможных выборах простого числа р ) . В каждом П. содержится единственное простое подполе (П. примеров 2—5 содержат П. рациональных чисел). Естественно было бы поставить такую задачу: отправляясь от простого П., получить описание всех П., изучив структуру расширений; приводимая ниже теорема Штейница делает шаг именно в этом направлении.

Некоторые расширения имеют сравнительно простое строение. Это — а) простые трансцендентные расширения, которые сводятся к тому, что за поле G берётся П. всех рациональных функций от одного переменного с коэффициентами из F, и б) простые алгебраические расширения (пример 5), которые получаются, если совокупность G всех многочленов степени n складывать и умножать по модулю данного неприводимого над F многочлена f ( x ) степени n (конструкция, аналогичная примеру 6). Расширения второго типа сводятся к тому, что мы добавляем к F корень многочлена f ( x ) и все те элементы, которые можно выразить через этот корень и элементы F; каждый элемент надполя G является корнем некоторого многочлена с коэффициентами из F. Расширения, обладающие последним свойством, называется алгебраическими. Любое расширение можно выполнить в два приёма: сначала совершить трансцендентное расширение (образовав П. рациональных функций, не обязательно от одной переменной), а затем алгебраическое (теорема Штейница). Алгебраических расширений не имеют только такие П., в которых каждый многочлен разлагается на линейные множители. Такие П. называются алгебраически замкнутыми. П. комплексных чисел является алгебраически замкнутым ( алгебры основная теорема ) . Любое П. можно включить в качестве подполя в алгебраически замкнутое.

Некоторые П. специального вида подверглись более детальному изучению. В теории алгебраических чисел рассматриваются главным образом простые алгебраические расширения П. рациональных чисел. В теории алгебраических функций исследуются простые алгебраические расширения П. рациональных функций с комплексными коэффициентами; значительное внимание уделяется конечным расширениям П. рациональных функций над произвольным П. констант (т. е. с произвольными коэффициентами). Конечные расширения П., в особенности их автоморфизмы (см. Изоморфизм ) , изучаются в теории Галуа (см. Галуа теория ) ; здесь находят ответ многие вопросы, возникающие при решении алгебраических уравнений. Во многих вопросах алгебры, особенно в различных отделах теории П., большую роль играют нормированные поля. В связи с геометрическими исследованиями появились и изучались упорядоченные П.

См. также Алгебра, Алгебраическое число, Алгебраическая функция, Кольцо алгебраическое.