БСЭ БСЭ - Большая Советская Энциклопедия (ПО)

С начала 20 в. в П. т. появляется новое направление, в котором исследуется поверхность «в целом» по данным свойствам окрестностей её точек. Например, Л. Г. Шнирельманом и Л. А. Люстерником было доказано существование трёх замкнутых геодезических на регулярных замкнутых поверхностях, гомеоморфных сфере. Продолжение гладких поверхностей иногда приводит к появлению на них особенностей. Например, всякая развёртывающаяся поверхность, не являющаяся цилиндрической, при продолжении доходит до ребра (или острия в случае конуса). Рассмотрение поверхностей во всём их протяжении и с особенностями (т. е. отказ от требований дифференцируемости) потребовало изобретения принципиально новых методов исследования поверхностей и привлечения методов из других разделов математики. Развитие П. т. в этом направлении привело к созданию содержательных разделов геометрии. Так, например, глубокие и принципиально новые результаты были получены А. Д. Александровым и А. В. Погореловым в теории выпуклых поверхностей. Александровым был предложен новый метод исследования выпуклых поверхностей, основанный на приближении выпуклых поверхностей выпуклыми многогранниками.

Рассмотренные свойства поверхностей не меняются при любых изометрических преобразованиях всего пространства, т. е. они относятся к т. н. метрической П. т. Изучают также свойства поверхностей, инвариантные по отношению к какой-либо другой группе преобразований пространства, например группе аффинных или проективных преобразований. Аффинная П. т. рассматривает свойства поверхностей, неизменные при эквиаффинных преобразованиях (аффинных преобразованиях, сохраняющих объём). Проективная П. т. рассматривает проективно-инвариантные свойства поверхностей.

Лит.: Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956; Норден А. П., Теория поверхностей, М., 1956; Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969; Каган В. Ф., Основы теории поверхностей в тензорном изложении, ч. 1—2, М. — Л., 1947—48; Бляшке В., Дифференциальная геометрия и геометрические основы теории относительности Эйнштейна, пер. с нем., т. 1, М. — Л., 1935; Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М. — Л., 1948; Погорелов А. В., Внешняя геометрия выпуклых поверхностей, М., 1969; Фиников С. П., Проективно-дифференциальная геометрия, М. — Л., 1937; Широков П. А., Широков А. П., Аффинная дифференциальная геометрия, М., 1959; Blaschke W., Vorlesungen Über Differentialgeometrie, Bd 2, В., 1923; Biarichi L., Lezioni di geometria differenziale, 3 éd., t. 1—2, Bologna, 1937; Darboux G., Leçons sur la théorie générale des surfaces, 2 éd., t. 1—4, P., 1924—25.

Э. Г. Позняк.

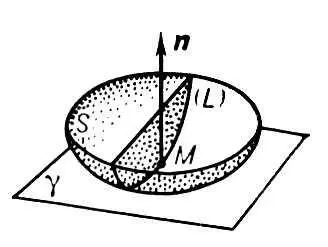
Рис. 1 к ст. Поверхностей теория.

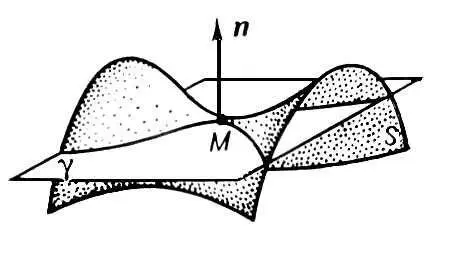
Рис. 2 к ст. Поверхностей теория.

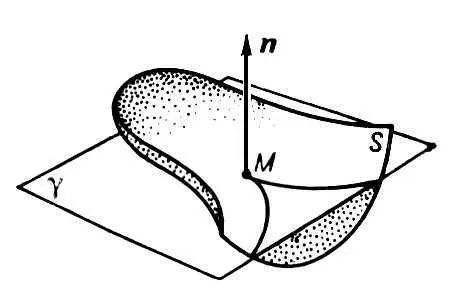
Рис. 3 к ст. Поверхностей теория.

Пове'рхности враще'ния, поверхности, образуемые вращением плоской кривой вокруг прямой (оси П. в.), расположенной в плоскости этой линии. Примером П. в. может служить сфера (которую можно рассматривать как поверхность, образованную вращением полуокружности вокруг её диаметра). Линии пересечения П. в. с плоскостями, проходящими через её ось, называется меридианами; линии пересечения П. в. с плоскостями, перпендикулярными оси, — параллелями. Если по оси П. в. направить ось Oz прямоугольной системы координат Oxyz, то параметрическое уравнения П. в. можно записать следующим образом:

x = f ( u ) cosu, y = f ( u ) sinu, z = u.

[здесь f ( u ) — функция, определяющая форму меридиана, а u — угол поворота плоскости меридиана].

Пове'рхности второ'го поря'дка, поверхности, декартовы прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2-й степени:

a 11 x 2+ a 22 y 2+ a 33 z 2+ 2 a 12 xy + 2 a 23 yz + 2 a 13 xz + 2 a 14 x + 2 a 24 y + 2 a 34 z + a 44= 0 (*)

Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую П. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из 17 приведённых ниже канонических видов, каждому из которых соответствует определённый класс П. в. п. Среди них выделяют пять основных типов поверхностей. Именно,

1) эллипсоиды

— эллипсоиды,

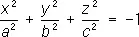— мнимые эллипсоиды;

2) гиперболоиды:

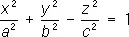— однополостные гиперболоиды,

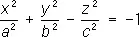— двуполостные гиперболоиды;

3) параболоиды ( p > 0, q > 0):

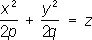— эллиптические параболоиды,

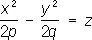— гиперболические параболоиды;

4) конусы второго порядка:

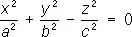— конусы,

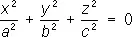— мнимые конусы;

5) цилиндры второго порядка:

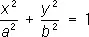— эллиптические цилиндры,

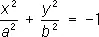— мнимые эллиптические цилиндры,

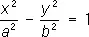— гиперболические цилиндры,

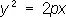— параболические цилиндры.

Перечисленные П. в. п. относятся к т. н. нераспадающимся П. в. п.; распадающиеся П. в. п.:

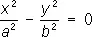— пары пересекающихся плоскостей,

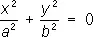—пары мнимых пересекающихся плоскостей,