БСЭ БСЭ - Большая Советская Энциклопедия (РА)

Лит.: Математика в СССР за 40 лет. 1917—1957, т. 2, М., 1959 (имеется лит.).

Разма'х— разность между наибольшим и наименьшим значениями результатов наблюдений. Пусть X 1 , ..., X n— взаимно независимые случайные величины с функцией распределения F ( x ) и плотностью вероятности f ( x ). В этом случае размах W nопределяется как разность между наибольшим и наименьшим значениями среди X 1, ..., X n ; размах W nпредставляет собой случайную величину, которой соответствует функция распределения:

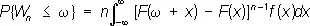
(w ³ 0; если w < 0 , то P { W £ w} = 0).

В математической статистике Р., надлежащим образом нормированный, применяется как оценка неизвестного квадратичного отклонения. Например, если X kимеют нормальное распределение с параметрами ( а , s), то при n = 5 и 10, соответственно, величины 0,4299 W 5 и 0,3249 W 10 будут несмещенными оценками s . Такие оценки часто используют при статистическом контроле качества, поскольку определение Р. нескольких результатов измерений не требует сложных вычислений.

Лит. : Хальд А. , Математическая статистика с техническими приложениями, пер. с англ., М., 1956.

Разме'рмузыкальный, метрический размер, тактовый размер, выражение музыкального метра в определённых ритмических единицах.

Разме'р едини'цыфизической величины, количественное содержание величины в единице. Размеры основных единиц какой-либо системы единиц устанавливаются при их выборе и определяют размеры всех производных единиц данной системы. Так, размер единиц площади и объёма зависит от выбора единицы длины. Для образования ряда единиц различного размера ( кратных единиц и дольных единиц ) данной величины используются десятичные приставки (см. Международная система единиц ). Размеры десятичных кратных и дольных единиц соотносятся как степени десяти, соответствующие приставкам, входящим в наименования единиц. Так, размер миллиметра в 1000 раз меньше размера метра.

Разме'р стихотво'рный,форма стихотворного ритма , последовательно выдержанная на протяжении стихотворного произведения или его отрывка. В силлабическом стихосложении Р. с. определяется числом слогов (8-сложный стих, 11-сложный стих); в тоническом стихосложении— числом ударений (3-ударный стих, 4-ударный стих); в метрическом стихосложении и силлабо-тоническом стихосложении— числом стоп (3-стопный ямб, 4-стопный дактиль). Обычно различаются понятия метр (определяющий ритмическое строение стиха, например ямб), Р. с. (определяющий длину стиха, например 4-стопный ямб) и разновидность Р. с. (определяющая дополнительную специфику ритма, например 4-стопный ямб со сплошными мужскими окончаниями или чередование 4-стопного и 3-стопного ямба). Однако эта терминология ещё не вполне установилась (в частности, термины «метр» и «Р. с.» иногда употребляются как синонимы).

Различные Р. с. по-разному соотносятся с членением речи на синтагмы и колоны и, следовательно, с её интонационным строением. Ближе всего совпадают со средним объёмом колона, допускают наиболее естественные и разнообразные интонации и поэтому наиболее употребительны в русской поэзии Р. с. с длиной строки в 8—9 слогов (4-стопные хорей и ямб, 3-стопные дактиль, анапест и амфибрахий); более короткие Р. с. звучат отрывисто, более длинные — торжественно и плавно. Эти естественные особенности во взаимодействии с историко-литературными традициями определяют тяготение отдельных Р. с. к тем или иным жанрам и темам. Так, 6-стопный ямб с парной рифмовкой ( александрийский стих ) в русской поэзии 18 в. употреблялся преимущественно в «высоких» жанрах классицизма (поэма, трагедия, дидактическое послание и др.), в 19 в. — в стихах на античные темы («антологическая лирика» А. А. Фета, А. Н. Майкова и др.) и в меньшей степени на гражданские темы («Элегия» Н. А. Некрасова), а в 20 в. теряет эти области применения и остаётся почти неупотребителен. Так, 4-стопный ямб со сплошными мужскими рифмами употреблялся почти исключительно в стихах, связанных (хотя бы пародически) с романтической традицией («Шильонский узник» В. А. Жуковского, «Мцыри» М. Ю. Лермонтова, «На Волге» и «Суд» Некрасова, «Мурманские дневники» К. М. Симонова).

В зависимости от популярности различных жанров и освоения различной тематики употребительность разных Р. с. в истории русской поэзии менялась. В силлабической поэзии 17—18 вв. господствовали размеры 11- и 13-сложный. В силлабо-тонической поэзии 18 в. безраздельно господствовали 6-стопный ямб, 4-стопный ямб, вольный ямб и 4-стопный хорей. В 1-й половине 19 в. постепенно входят в употребление 5-стопный ямб и трёхсложные размеры (дактиль, амфибрахий, анапест, сначала чаще 4-стопные, потом 3-стопные). Во 2-й половине 19 в. складываются относительно устойчивые пропорции употребления Р. с. в русской лирике: около четверти всех стихотворений пишется 4-стопным ямбом, четверть — остальными ямбическими Р. с., четверть — хореями, четверть — 3-сложнымн размерами. В 20 в. в употребление входят несиллабо-тонические размеры — дольник (3- и 4-иктный), акцентный стих (3- и 4-ударный) и др.; в остальном пропорции групп Р. с. остаются теми же, хотя отдельные Р. с. к настоящему времени почти сходят со сцены (вольный ямб, 6-стопный ямб), а иные, наоборот, усиленно развиваются (5-стопный хорей).

Лит. см. при ст. Стихосложение.

М. Л. Гаспаров.

Разме'рностей ана'лиз,метод установления связи между физическими величинами, существенными для изучаемого явления, основанный на рассмотрении размерностей этих величин.

В основе Р. а. лежит требование, согласно которому уравнение, выражающее искомую связь, должно оставаться справедливым при любом изменении единиц входящих в него величин. Это требование совпадает с требованием равенства размерностей в левой и правой частях уравнения. Формула размерности физической величины имеет вид:

[ N ] = L lM mT t..., (1)

где [ N ] — символ размерности вторичной величины (обычно берётся в прямые скобки); L, М, Т, . .. — символы величин, принятых за основные (соответственно длины, массы, времени и т.д.); I, m, t, ... — целые или дробные, положительные или отрицательные вещественные числа. Показатели степени в формуле (1), т. е . числа l, m, t, называются показателями размерности или размерностью производной величины [ N ]. Так, формула размерности для ускорения (символ а ) записывается в виде [ а ] = LT —2, для силы — [ F ] = LMT —2 . Понятие размерности распространяется и на основные величины. Принимают, что размерность основной величины в отношении самой себя равна единице и что от др. величин она не зависит; тогда формула размерности основной величины совпадает с её символом. Если единица производной величины не изменяется при изменении какой-либо из основных единиц, то такая величина обладает нулевой размерностью по отношению к соответствующей основной. Так, ускорение обладает нулевой размерностью по отношению к массе. Величины, в размерность которых все основные величины входят в степени, равной нулю, называются безразмерными. Выбор числа физических величин, принимаемых за основные, и самих этих величин в принципе произволен, но практические соображения приводят к некоторому ограничению свободы в выборе основных величии и их единиц.