БСЭ БСЭ - Большая Советская Энциклопедия (РА)

Согласно Венской конвенции 1961 о дипломатических сношениях при Р. д. о. государство пребывания должно оказать содействие для возможно скорого выезда на родину сотрудников дипломатического представительства и членов их семей.

Государства, порвавшие дипломатические отношения, могут поддерживать контакты по некоторым, обычно текущим делам через представительства какого-либо третьего государства, которому эти государства вверяют защиту своих интересов и интересов своих граждан, охрану помещений отзываемого представительства, его имущества и архивов.

В практике империалистических держав Р. д. о. или угроза Р. д. о. нередко используются как средство вмешательства во внутренние дела других государств, как средство политического давления и провокации международных конфликтов (например, Р. д. о. США и рядом латиноамериканских стран с Кубой в 1961—62).

Устав ООН допускает Р. д. о. как возможную коллективную меру, осуществляемую государствами по решению Совета Безопасности ООН.

Разры'ва то'чка,значение аргумента, при котором нарушается непрерывность функции (см. Непрерывная функция ). В простейших случаях нарушение непрерывности в некоторой точке а происходит так, что существуют пределы

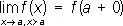
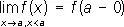
при стремлении x к а справа и слева, но хотя бы один из этих пределов отличен от f (a). В этом случае а называют Р. т. 1-го рода. Если при этом f ( a + 0) = f ( a — 0), то разрыв называется устранимым, так как функция f ( x ) становится непрерывной в точке а, если положить f ( a ) = f ( a + 0) = f ( a — 0). Например, точка а = 0 является точкой устранимого разрыва для функции f ( x ) = 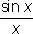при х ¹ 0 и f (0) = 0, так как для восстановления непрерывности достаточно положить f (0) = 1. Если же скачок d = f ( a +0) — f ( a — 0) функции f ( x ) в точке а отличен от нуля, то при любом определении значения f (a) точка а остаётся Р. т. Примером такой Р. т. служит точка а = 0 для функции f ( x ) = arctg 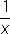(в этом случае в самой точке а функция может оставаться неопределённой). Р. т. 1-го рода называется правильной, если

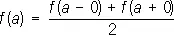
Если хотя бы один из односторонних пределов не существует, то а называется Р. т. 2-го рода [примеры: точка а = 2 для функции 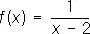, точка а = 0 для функции ] .

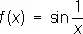Разрывна'я маши'наиспытательная, служит для определения механических свойств материалов, а также для испытаний деталей, сборочных единиц и изделий путём повреждения или разрушения. Р. м. имеет нагружающее устройство и измерительные приборы. По виду нагружающего устройства Р. м. разделяются на Р. м. с гидравлическим и механическим (рычажным, одно- и многошпиндельным) нагружающим устройством. Для испытания упругих материалов (металлы, древесина, резина, полимеры, ткани и др.) применяют Р. м. с одной или несколькими постоянными скоростями деформирования, а для испытания хрупких материалов — Р. м. с постоянной скоростью нагружения. По направлению растягивающего усилия Р. м. делятся на вертикальные и горизонтальные. Нагружающее устройство (механическое или гидравлическое) обеспечивает повторные циклические нагрузки. Измерительные приборы регистрируют усилия и деформации на различных стадиях испытаний. Приборы для измерения усилия могут быть механическими (рычажными, рычажно-маятниковыми, пружинными) и гидравлическими. Использование электронных схем позволяет автоматически воспроизводить заданный режим испытаний. Р. м. для испытания материалов при температуре, отличной от нормальной, снабжены печами и криокамерами (для охлаждения образца), Р. м., на которых можно проводить испытания не только на растяжение, но и на сжатие, изгиб, ползучесть, длительную прочность и релаксацию, называются универсальными (кинематическая схема советской универсальной Р. м. Р-5 приведена на рис. ). Такие Р. м. имеют диаграммный аппарат, записывающий процесс в координатах «нагрузка — деформация», «нагрузка — время», «деформация — время». Запись деформации производится от подвижного захвата или от тензометра , установленного на образце. Предельное усилие нагружающих устройств Р. м. для неметаллов — 10 5 н (10 4 кгс ), для металлов — 5·10 5 н (5·10 4 кгс ), для изделий — более 3·10 7 н (3·10 6 кгс ). Погрешности показаний приборов для измерения усилия ± 1%, а погрешность записи на диаграммном аппарате ±2%. См. также Усталости предел металлов.

Лит.: см. при ст. Механические свойства материалов .

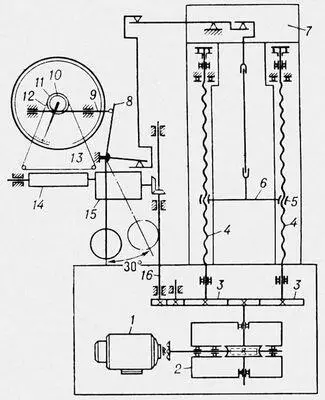
Кинематическая схема разрывной машины Р-5: 1 — электродвигатель; 2 — силовой редуктор; 3 — цилиндрические шестерни; 4 — вращающиеся винты; 5 — гайки подвижной траверсы; 6 — подвижная траверса; 7 — неподвижная траверса; 8 — поводок; 9 — рейка; 10 — шестерня реечной передачи; 11 — шкив; 12 — тросик; 13 — перо; 14 — барабан лентопротяжного механизма; 15 — редуктор масштаба записи; 16 — валик.

Разрывны'е колеба'ния,колебания, при которых наряду со сравнительно медленными изменениями величин, характеризующих состояние колебательной системы, в некоторые моменты происходят столь быстрые изменения этих величин, что их можно рассматривать как скачки, а весь колебательный процесс в целом — как последовательность медленных изменений состояния системы, начинающихся и кончающихся мгновенным изменением состояния системы (скачками или разрывами). Релаксационные колебания часто рассматривают как Р. к.

Разры'вные фу'нкции,функции, имеющие разрыв в некоторых точках (см. Разрыва точка ). Обычно у функций, встречающихся в математике, точки разрыва изолированы, но существуют функции, для которых все точки являются точками разрыва, например функция Дирихле: f ( x ) = 0, если х рационально, и f ( x ) = 1, если х иррационально. Предел всюду сходящейся последовательности непрерывных функций может быть Р. ф. Такие Р. ф. называются функциями первого класса по Бэру. Французский математик Р. Бэр дал классификацию Р. ф. (см. Бэра классификация ). Важным классом Р. ф. являются измеримые функции. А. Лебег построил теорию интегрирования Р. ф. Н. Н. Лузин показал, что путём изменения значений измеримой функции на множестве сколь угодно малой меры (см. Мера множества ) её можно превратить в непрерывную функцию. Если функция монотонна, то она имеет лишь разрывы 1-го рода. Для функций нескольких переменных наряду с отдельными точками разрыва приходится рассматривать линии, поверхности и т.д. разрыва.