БСЭ БСЭ - Большая Советская Энциклопедия (РА)

т. е., например, для непрерывного Р.

D X =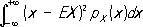

Р. вероятностей имеют много общего с Р. каких-либо масс на прямой. Так, случайной величине X , принимающей значения x 1 x 2 ..., x nc вероятностями p 1, p 2 , ..., p n , можно поставить в соответствие Р. масс, при котором в точках x kразмещены массы, равные p k . При этом формулы для E X и D X оказываются совпадающими с формулами, определяющими соответственно центр тяжести и момент инерции указанной системы материальных точек. Подробнее о числовых характеристиках Р. см. в статьях Квантиль , Медиана , Мода , Математическое ожидание , Вероятное отклонение , Дисперсия , Квадратичное отклонение.

Если складываются несколько независимых случайных величин, то их сумма будет случайной величиной, Р. которой зависит только от Р. слагаемых (чего не будет, как правило, при сложении зависимых случайных величин). При этом, например, для случая двух слагаемых, каждое из которых имеет Р. непрерывного типа, имеет место формула:

(*)

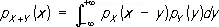В весьма широких предположениях Р. суммы независимых случайных величин при увеличении числа слагаемых приближается к нормальному Р. или к др. предельным Р. (см. Предельные теоремы теории вероятностей). Однако для установления этого факта явные формулы типа (*) практически непригодны, поэтому доказательство ведётся обходным путём, обычно с использованием т. н. характеристических функций.

Статистические распределения и их связь с вероятностными.Пусть произведено n независимых наблюдений случайной величины X , имеющей функцию Р. F ( x ) . Статистическое Р. результатов наблюдений задаётся указанием наблюдённых значений x 1, x 2, ..., x rслучайной величины Х и соответствующих им частот h 1 , h 2 , ..., h r(т. е. отношений числа наблюдений, в которых появляется данное значение, к общему числу наблюдений). Например, если при 15 наблюдениях значение 0 наблюдалось 8 раз, значение 1 наблюдалось 5 раз, значение 2 наблюдалось 1 раз и значение 3 наблюдалось 1 раз, то соответствующее статистическое Р. задаётся табличкой:

Частоты всегда положительны и в сумме дают единицу. С заменой слова «вероятность» на слово «частота» к статистическому Р. применимы многие определения, данные выше для Р. вероятностей. Так, если x 1 , x 2 , ..., x r — наблюдённые значения X , a h 1 , h 2 , ..., h r — частоты этих наблюдённых значений, то соответствующие статистическому Р. среднее и дисперсия (т. н. выборочное среднее и выборочная дисперсия) определяются равенствами

,

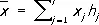
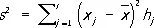а соответствующая функция Р. (т. н. эмпирическая функция распределения) — равенством

F* ( x ) = n x/ n ,

где n x — число наблюдений, результат которых меньше х. Статистическое Р. и его характеристики могут быть использованы для приближённого представления теоретического Р. и его характеристик. Так, например, если Х имеет конечные математическое ожидание и дисперсию, то, каково бы ни было e > 0, неравенства

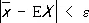
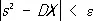
выполняются при достаточно большом n с вероятностью, сколь угодно близкой к единице. Т. о., 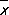и s 2суть состоятельные оценки для E X и D X соответственно (см. Статистические оценки ). Советский математик В. И. Гливенко показал, что при любом e > 0 вероятность неравенства

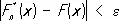
при всех x стремится к единице при n , стремящемся к бесконечности. Более точный результат установлен сов. математиком А. Н. Колмогоровым; см. об этом Непараметрические методы в математической статистике.

Многомерные распределения.Пусть Х и Y — две случайные величины. Каждой паре ( X, Y ) можно отнести точку Z на плоскости с координатами Х и Y , положение которой будет зависеть от случая. Совместное Р. величин Х и Y задаётся указанием возможных положений точки Z и соответствующих вероятностей. Здесь также можно выделить два основных типа Р.

1) Дискретные распределения. Возможные положения точки Z образуют конечную или бесконечную последовательность. Р. задаётся указанием возможных положений точки Z

z 1 , z 2 , ..., z n , ...

и соответствующих вероятностей p 1, p 2 , ..., p n , ...

2) Непрерывные распределения задаются плотностью вероятности р ( x , у ), обладающей тем свойством, что вероятность попадания точки Z в какую-либо область G равна

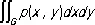
Пример: двумерное нормальное Р. с плотностью

,

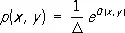где

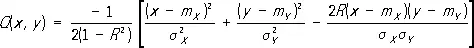
m X= E X , m Y = EY,

,

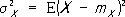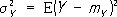
— математические ожидания и дисперсии величин Х и Y ,

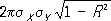
и R — коэффициент корреляции величин Х и Y :

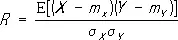
Аналогично можно рассматривать Р. вероятностей в пространствах трёх и большего числа измерений. О многомерных Р. см. также Корреляция , Регрессия.

О возможности дальнейших обобщений и о связи между понятием меры множества и понятием Р. см. Вероятностей теория.