БСЭ БСЭ - Большая Советская Энциклопедия (РА)

Подобным же образом Р. любой случайной величины X , возможные значения которой образуют конечную или бесконечную последовательность, задаётся указанием этих значений

x 1 , x 2 , ..., x n , ...

и соответствующих им вероятностей

p 1 , p 2 , ..., p n , ...

При этом вероятности p mдолжны быть положительны и в сумме должны давать единицу. Р. указанного типа называются дискретными. Примером дискретного Р. может служить Пуассона распределение , определяемое вероятностями

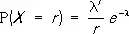, r = 0, 1, 2, …,

где l > 0— параметр.

Однако задание Р. указанием возможных значений x nи соответствующих вероятностей p nне всегда возможно. Например, если величина распределена «равномерно» на отрезке [— 1/ 2, + 1/ 2], подобно «ошибкам округления» при измерении непрерывных величин, то вероятность каждого отдельного значения равна нулю. Р. таких случайных величин задаётся указанием вероятности того, что случайная величина Х примет значение из любого наперёд заданного интервала. В том случае, когда существует функция p X( x ) такая, что вероятность попадания Х в любой интервал ( а , b ) равна

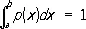
Р. величины Х называется непрерывным. Функция p X( x ) носит название плотности вероятности. Плотность вероятности неотрицательна и обладает тем свойством, что

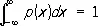
В указанном выше случае равномерного Р. на отрезке [— 1/ 2, + 1/ 2]

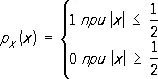
Важнейшее Р. непрерывного типа — нормальное распределение с плотностью

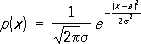
( а и s > 0 — параметры).

Р. случайных величин не исчерпываются дискретным и непрерывным типами: они могут быть и более сложной природы. Поэтому желательно иметь такое описание Р., которое было бы пригодно во всех случаях. Это описание может быть достигнуто, например, при помощи т. н. функции распределения F X ( x ). Значение этой функции при каждом фиксированном х равно вероятности Р { Х < х } того, что случайная величина х примет значение, меньшее x, т. е.

F X ( x ) = Р { Х < x }.

Функция Р. есть неубывающая функция x, изменяющаяся от 0 до 1 при изменении х от — ¥ до + ¥. Вероятность того, что Х примет значение из некоторого полуинтервала [ a , b ), равна вероятности того, что Х будет удовлетворять неравенству а £ Х < b, т. е. равна

F ( b ) - F ( a ).

Примеры. 1) Пусть Е — некоторое событие, вероятность появления которого есть р , где 0 < р < 1. Тогда число m появлений события Е при n независимых наблюдениях есть случайная величина, принимающая значения m = 0, 1, 2, ..., n с вероятностями

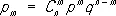( q = 1 - p )

Это Р. носит название биномиального распределения. Биномиальное Р. (см. рис. 1 , а и б) при больших n близко к нормальному в силу Лапласа теоремы.

2) Число наблюдений до первого появления события Е из примера 1 есть случайная величина, принимающая все целые значения m = 1, 2, 3, ... с вероятностями

p m= q m - 1 p.

Это Р., носит название геометрического, т.к. последовательность { pm } есть геометрическая прогрессия (см. рис. 2 , а и б).

3) Р., плотность которого р ( х ) равна 1/ 2 h на некотором интервале ( а — h , а + h ) и равна нулю вне этого интервала, носит название равномерного распределения. Соответствующая функция Р. растет линейно от 0 до 1 при изменении х от а — h до а + h (см. рис. 3 , а и б).

Дальнейшие примеры Р. вероятностей см. в статьях Коши распределение , Пирсона кривые , Полиномиальное распределение , Показательное распределение , «Хи-квадрат» распределение , Стьюдента распределение.

Пусть случайные величины Х и Y связаны соотношением Y = f ( X ), где f ( x ) — заданная функция. Тогда Р. Y может быть довольно просто выражено через Р. X . Например, если Х имеет нормальное Р. и Y = e X, то Y имеет т. н. логарифмически-нормальное распределение с плотностью (см. рис. 4 )

.

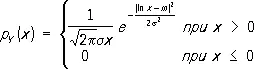Формулы, связывающие Р. величин X и Y, становятся особенно простыми, когда Y = aX + b , где а и b — постоянные. Так, при a > 0

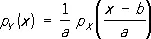
Часто полное описание Р. (например, при помощи плотности или функции Р.) заменяют заданием небольшого числа характеристик, которые указывают или на наиболее типичные (в том или ином смысле) значения случайной величины, или на степень рассеяния значений случайной величины около некоторого типичного значения. Из этих характеристик наиболее употребительны математическое ожидание (среднее значение) и дисперсия. Математическое ожидание E X случайной величины X , имеющей дискретное Р., определяется как сумма ряда

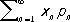
при условии, что этот ряд сходится абсолютно. Для случайной величины X , имеющей Р. непрерывного типа с плотностью p X( x ), математическое ожидание определяется формулой

E X =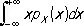

при условии, что написанный интеграл сходится абсолютно. Если Y = f ( X ), то E Y может быть вычислено двумя способами. Например, если Х и Y имеют непрерывное Р., то, с одной стороны, по определению

E Y =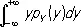

с другой стороны, можно показать, что

E Y =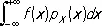

Дисперсия D X определяется как

D X = Е ( Х — E X ) 2 ,