БСЭ БСЭ - Большая Советская Энциклопедия (РЯ)

Ря'бчик(Tetrastes bonasia), птица семейства тетеревиных отряда куриных. Длина тела 35—37 см, весит 350—500 г. Крылья короткие, тупые. Взлетает с шумом, летает лишь на небольшие расстояния. Нижняя часть цевки и пальцы голые. Оперение рыжевато-серое с пестринами, у Р., обитающих в Сибири, — более чистого серого тона. Распространён в Европе и Азии; в СССР — в лесной зоне от Карпат до Сахалина; в лесах Кавказа и Камчатки отсутствует. Р. живут оседло, совершая лишь короткие кормовые кочёвки. Селятся отдельными парами в сырых захламлённых хвойных (елово-пихтовых) или смешанных лесах. Гнёзда на земле; в кладке 6—10 яиц, насиживает самка около 3 недель. Птенцы достигают размеров взрослых Р. через 6 недель после вылупления. Первое время они питаются насекомыми, потом растительным кормом. Зимой Р. кормятся на деревьях серёжками берёзы, ольхи и др., ночуют в снегу. Основные корма летом: зелёные части растений, ягоды, семена и насекомые. Р. — ценная промысловая птица.

Рябчик: 1 — самец; 2 — самка.

Ря'бчик(Fritillaria), род луковичных растений семейства лилейных. Луковица округлая, чаще из 2—4 мясистых чешуй; стебель облиственный, листорасположение очередное или мутовчатое. Цветки обычно крупные, одиночные или по нескольку на верхушке стебля; околоцветник из 6 листочков с нектарниками у основания, колокольчатый или кубаревидный, беловатый, жёлтый, оранжевый, коричневатый, нередко с шахматным рисунком. Плод — 6-гранная, иногда крылатая коробочка. Около 100 видов, в умеренных областях обоих полушарий. В СССР около 30 видов, чаще на Кавказе и в Средней Азии, а также в Европейской части (лесостепь и степь), Западной Сибири и на Дальнем Востоке, на лугах, в степях, среди кустарников, по склонам гор в субальпийском и альпийском поясах. Все виды Р. декоративны, цветут весной; наиболее известны Р. шахматный (F. теleagris) и Р. императорский (F. imperialis).

Ря'вала,прибрежная земля (мааконд) в Северной Эстонии (ныне Харьюский район Эстонской ССР), состоявшая из трёх территориальных объединений (кихелькондов). Центром Р. в 11—13 вв. была крепость, известная под названием Колывань или Линданисе. Под датской властью Р. была объединена с землёй Харью под название Харьюмаа (Гарриен). От названия земли Р. происходит старое название Таллина — Ревель (Reval).

Лит.: История Эстонской ССР, т. 1, Тал., 1961; Johansen P., Die Estlandliste des Liber census Daniae, Kph. — Reval, 1933.

Ряд акти'вностей,то же, что ряд напряжений .

Ряд,бесконечная сумма, например вида

u 1+ u 2 + u 3+... + u n+...

или, короче,

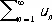. (1)

Одним из простейших примеров Р., встречающихся уже в элементарной математике, является сумма бесконечно убывающей геометрической прогрессии

1 + q + q 2 +... + q n +... = 1/(1 - q ), ½ q ½< 1. (2)

Р. широко используются в математике и её приложениях как в теоретических исследованиях, так и при приближённых численных решениях задач. Многие числа могут быть записаны в виде специальных Р., с помощью которых удобно вычислять их приближённые значения с нужной точностью. Например, для числа p имеется Р.

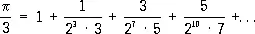, (3)

для основания е натуральных логарифмов — Р.

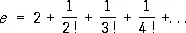, (4)

а для натурального логарифма In2 — ряд

.

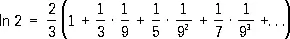Метод разложения в Р. является эффективным методом изучения функций. Он применяется для вычисления приближённых значений функций, для вычисления и оценок интегралов, для решения всевозможных уравнений (алгебраических, дифференциальных, интегральных) и т. п.

При численных расчётах, когда Р. заменяется конечной суммой его первых слагаемых, полезно иметь оценку получаемой при этом погрешности (оценку «скорости сходимости» Р.). При этом целесообразно использовать Р., у которых эти погрешности достаточно быстро стремятся к нулю с возрастанием номера n. Например, в случае Р. (4) оценка указанной погрешности имеет вид 0 < е — s n < 1 /n ! n.

Одни и те же величины могут выражаться через суммы различных рядов. Так, для числа p, кроме Р. (3), имеются и другие Р., например

,

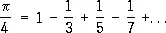однако он сходится значительно «медленнее» Р. (3), и потому его невыгодно использовать для приближённого вычисления числа p . Существуют методы преобразования Р., иногда улучшающие скорость сходимости Р.

На бесконечные суммы не переносятся все свойства конечных сумм. Например, если взять Р.

1 - 1 + 1 - 1 +... (5)

и сгруппировать подряд его члены по два, то получим (1—1) + (1—1) +... = 0; при другом же способе группировки 1 — (1 — 1) — (1 — 1) —... = 1. Поэтому следует дать чёткое определение того, что называется бесконечной суммой, и, определив это понятие, проверить, справедливы ли для таких сумм закономерности, установленные для конечных сумм. Доказывается, что для бесконечного числа слагаемых при определённых условиях сохраняются законы коммутативности и ассоциативности сложения, дистрибутивности умножения относительно сложения, правила почленного дифференцирования и интегрирования и т. п.

Числовые ряды.Формально Р. (1) можно определить как пару числовых (действительных или комплексных) последовательностей { u n } и { S n} таких, что S n = u 1+... + u n, n = 1, 2,... Первая последовательность называется последовательностью членов Р., а вторая — последовательностью его частичных сумм [точнее S nназывается частичной суммой n- го порядка Р. (1)]. Р. (1) называется сходящимся, если сходится последовательность его частичных сумм { S n} . В этом случае предел

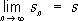
называется суммой Р. и пишется

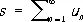
Т. о., обозначение (1) применяется как для самого Р., так и для его суммы (если он сходится). Если последовательность частичных сумм не имеет предела, то Р. называется расходящимся. Примером сходящегося Р. является Р. (2), расходящегося — Р. (5). Каждый Р. однозначно определяет последовательность его частичных сумм, и обратно: для любой последовательности { s n} имеется и притом единственный Р., для которого она является последовательностью его частичных сумм, причём члены u nэтого Р. определяются по формулам u 1 = s 1,..., u n+1 = s n + 1 — s n ,..., n = 1, 2,... В силу этого изучение Р. эквивалентно изучению последовательностей.