БСЭ БСЭ - Большая Советская Энциклопедия (РЯ)

Если в этом Р. переставить члены так, чтобы за двумя положительными следовал один отрицательный:

,

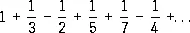то его сумма увеличится в 1,5 раза. Существуют признаки сходимости, применимые к не абсолютно сходящимся Р. Например, признак Лейбница: если

, ,

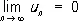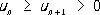то знакочередующийся Р.

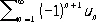(10)

сходится. Более общие признаки можно получить, например, с помощью преобразования Абеля для Р., представимых в виде

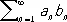. (11)

Признак Абеля: если последовательность { a n} монотонна и ограничена, а Р.

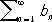
сходится, то Р. (11) также сходится. Признак Дирихле: если последовательность { a n} монотонно стремится к нулю, а последовательность частичных сумм Р.

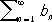
ограничена, то Р. (11) сходится. Например, по признаку Дирихле Р.

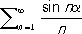
сходится при всех действительных a .

Иногда рассматриваются Р. вида

.

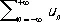Такой Р. называется сходящимся, если сходятся Р.

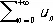и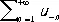

сумма этих Р. называется суммой исходного Р.

Р. более сложной структуры являются кратные ряды, т. е. Р. вида

,

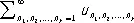где 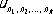— заданные числа (вообще говоря, комплексные), занумерованные k индексами, n 1, n 2,..., n k , каждый из которых независимо от других пробегает натуральный ряд чисел. Простейшие из Р. этого типа — двойные ряды.

Для некоторых числовых Р. удаётся получить простые формулы для величины или оценки их остатка, что весьма важно, например, при оценке точности вычислений, проводимых с помощью Р. Например, для суммы геометрической прогрессии (2)

r n= q n+ 1/(1 - q ), ½ q ½< 1,

для P. (7) при сделанных предположениях

,

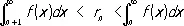а для P. (10)

½ r n½ £ u n+1

С помощью некоторых специальных преобразований иногда удаётся «улучшить» сходимость сходящегося Р. В математике используются не только сходящиеся Р., но и расходящиеся. Для последних вводятся более общие понятия суммы Р. (см. Суммирование рядов и интегралов). Так, например, расходящийся Р. (5) можно просуммировать определённым способом к 1/ 2.

Функциональные ряды. Понятие Р. естественным образом обобщается на случай, когда членами Р. являются функции u n = u n ( x ) (действительные, комплексные или, более общо, функции, значения которых принадлежат какому-то метрическому пространству), определённые на некотором множестве Е. В этом случае ряд

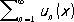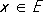, (11)

называется функциональным.

Если Р. (11) сходится в каждой точке множества Е, то он называется сходящимся на множестве Е. Пример: Р. 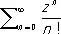сходится на всей комплексной плоскости. Сумма сходящегося Р. непрерывных, например, на некотором отрезке, функций не обязательно является непрерывной функцией. Условия, при которых на функциональные Р. переносятся свойства непрерывности, дифференцируемости и интегрируемости конечных сумм функций, формулируются в терминах равномерной сходимости Р. Сходящийся Р. (11) называется равномерно сходящимся на множестве Е, если во всех точках Е отклонение частичных сумм Р.

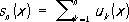
при достаточно больших номерах n от суммы Р.

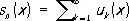
не превышает одной и той же сколь угодно малой величины, точнее, каково бы ни было наперёд заданное число e > О, существует такой номер n e, что

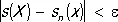
для всех номеров n £ n eи всех точек х Î Е. Это условие равносильно тому, что

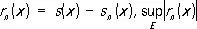[ — верхняя грань 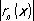на Е ] . Например, Р.

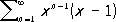
равномерно сходится на отрезке [0, q ] при 0 < q < 1 и не сходится равномерно на отрезке [0, 1].

Критерий Коши: для того чтобы Р. (11) равномерно сходился на множестве Е, необходимо и достаточно, чтобы для любого e > 0 существовал такой номер n e, что для всех номеров п ³ n e, р … 0 и всех точек 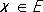выполнялось неравенство

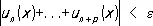
Признак Вейерштрасса: если существует такой сходящийся числовой Р.

,

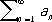что 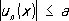ê , 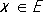, n = 1, 2,..., то Р. (11) равномерно сходится на Е.

Сумма равномерно сходящегося Р. непрерывных на некотором отрезке (или, более общо, на некотором топологическом пространстве) функций является непрерывной на этом отрезке (пространстве) функцией. Сумма равномерно сходящегося Р. интегрируемых на некотором множестве функций является интегрируемой на этом множестве функцией, и Р. можно почленно интегрировать. Если последовательность частичных сумм Р. интегрируемых функций сходится в среднем к некоторой интегрируемой функции, то интеграл от этой почти всюду сходящейся последовательностью частичных сумм является равномерной функции равен сумме Р. из интегралов от членов Р. Интегрируемость в этих теоремах понимается в смысле Римана или Лебега. Для интегрируемых по Лебегу функций достаточным условием возможности почленного интегрирования Р. с почти всюду сходящейся последовательностью частичных сумм является равномерная оценка их абсолютных величин некоторой интегрируемой по Лебегу функцией. Если члены сходящегося на некотором отрезке Р. (11) дифференцируемы на нём и Р. из их производных сходится равномерно, то сумма Р. также дифференцируема на этом отрезке и Р. можно почленно дифференцировать.