БСЭ БСЭ - Большая Советская Энциклопедия (СХ)

Сходи'мости то'чкафункционального ряда 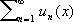, такая точка x 0 , что числовой ряд 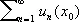, составленный из значений функции u n (x) в данной точке x 0 , является сходящимся. Аналогично определяется С. т. для функциональной последовательности.

Сходи'мость,математическое понятие, означающее, что некоторая переменная величина имеет предел. В этом смысле говорят о С. последовательности, С. ряда, С. бесконечного произведения, С. непрерывной дроби, С. интеграла и т. д. Понятие С. возникает, например, когда при изучении того или иного математического объекта строится последовательность более простых в известном смысле объектов, приближающихся к данному, то есть имеющих его своим пределом (так, для вычисления длины окружности используется последовательность длин периметров правильных многоугольников, вписанных в окружность; для вычисления значений функций используются последовательности частичных сумм рядов, которыми представляются данные функции, и т. п.).

С. последовательности { an } , n = 1, 2,..., означает существование у неё конечного предела 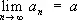; С. ряда 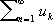— конечного предела (называемого суммой ряда) у последовательности его частичных сумм 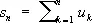, 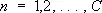; С. бесконечного произведения b 1b 2... b n— конечного предела, не равного нулю, у последовательности конечных произведений p n= b 1b 2... b n, n = 1, 2,...; С. интеграла 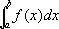от функции f ( x ) , интегрируемой по любому конечному отрезку [ а, b ] ,— конечного предела у интегралов при b ® +µ, называется несобственным интегралом .

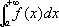Свойство С. тех или иных математических объектов играет существенную роль как в вопросах теории, так и в приложениях математики. Например, часто используется представление каких-либо величин или функций с помощью сходящихся рядов; так, для основания натуральных логарифмов е имеется разложение его в сходящийся ряд

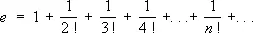
для функции sin х — в сходящийся при всех х ряд

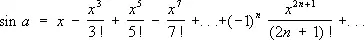
Подобные ряды могут быть использованы для приближённого вычисления рассматриваемых величин и функций. Для этого достаточно взять сумму нескольких первых членов, при этом чем больше их взять, тем с большей точностью будет получено нужное значение. Для одних и тех же величин и функций имеются различные ряды, суммой которых они являются, например,

,

.

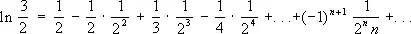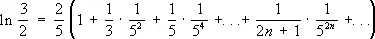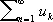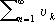При практических вычислениях в целях экономии числа операций (а следовательно, экономии времени и уменьшения накопления ошибок) целесообразно из имеющихся рядов выбрать ряд, который сходится «более быстро». Если даны два сходящихся ряда и , и 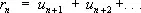, 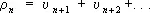. — их остатки, то 1-й ряд называется сходящимся быстрее 2-го ряда, если

.

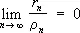Например, ряд

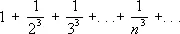
сходится быстрее ряда

.

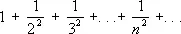Используются и другие понятия «более быстро» сходящихся рядов. Существуют различные методы улучшения С. рядов, то есть методы, позволяющие преобразовать данный ряд в «более быстро» сходящийся. Аналогично случаю рядов вводится понятие «более быстрой» С. и для несобственных интегралов, для которых также имеются способы улучшения их С.

Большую роль понятие С. играет при решении всевозможных уравнений (алгебраических, дифференциальных, интегральных), в частности при нахождении их численных приближённых решений. Например, с помощью последовательных приближений метода можно получить последовательность функций, сходящихся к соответствующему решению данного обыкновенного дифференциального уравнения, и тем самым одновременно доказать существование при определённых условиях решения и дать метод, позволяющий вычислить это решение с нужной точностью. Как для обыкновенных дифференциальных уравнений, так и уравнений с частными производными существует хорошо разработанная теория различных сходящихся конечноразностных методов их численного решения (см. Сеток метод ) . Для практического нахождения приближённых решений уравнений широко используются ЭВМ.

Если изображать члены a n последовательности { a n } на числовой прямой, то С. этой последовательности к а означает, что расстояние между точками a n и а становится и остаётся сколь угодно малым с возрастанием n. В этой формулировке понятие С. обобщается на последовательности точек плоскости, пространства и более общих объектов, для которых может быть определено понятие расстояния, обладающее обычными свойствами расстояния между точками пространства (например, на последовательности векторов, матриц, функций, геометрических фигур и т. д., см. Метрическое пространство ) . Если последовательность { a n } сходится к а, то вне любой окрестности точки а лежит лишь конечное число членов последовательности. В этой формулировке понятие С. допускает обобщение на совокупности величин ещё более общей природы, в которых тем или иным образом введено понятие окрестности (см. Топологическое пространство ) .