БСЭ БСЭ - Большая Советская Энциклопедия (СИ)
- Название:Большая Советская Энциклопедия (СИ)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (СИ) краткое содержание
Большая Советская Энциклопедия (СИ) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Синус аорты
Си'нус ао'рты(от лат. sinus — изгиб, пазуха, выпуклость), пазуха аорты, 1) у млекопитающих животных — начальная, расширенная часть восходящей аорты, то же, что аортальная луковица. 2) У человека — часть полости луковицы аорты, расположенная между полулунным клапаном и стенкой аорты.
Синус-верзус
Си'нус-ве'рзус(лат. sinus versus, буквально — обращенный синус), тригонометрическая функция аргумента а, применявшаяся как самостоятельная функция до 17 в. и в настоящее время весьма малоупотребительная. Обозначение sin vers a; С.-в. угла а равен 1 — cos a.
Синусная линейка
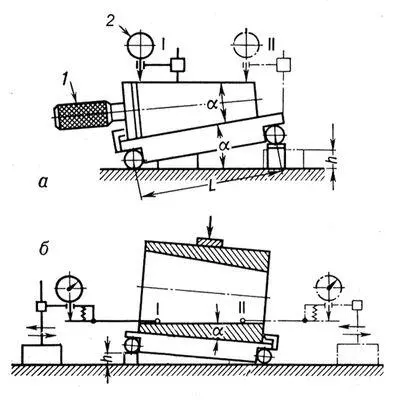
Си'нусная лине'йка,специальная линейка в виде прямоугольного параллелепипеда с двумя цилиндрическими роликами (шариками) на концах. С. л. предназначается для установки заданного угла при изготовлении или измерении деталей (например, конусов, клиньев и т. п.). С. л. располагается на плите, под один ролик плиты устанавливается блок концевых мер длины, размер h которых подсчитывают по формуле h = L sin a, где a — угол, на который требуется установить плоскость С. л., L — расстояние между осями роликов. Расстояния между роликами обычно от 100 до 500 мм, установка угла (наклона) в одном, или двух взаимно перпендикулярных направлениях. Измеряемая или обрабатываемая деталь устанавливается на плоской поверхности С. л. (или в центрах). Наиболее часто С. л. используют вместе с отсчётной головкой для определения погрешности угла у конусных калибров ( рис. ). С. л. настраивают на номинальный угол конуса, а по шкале отсчётной головки определяют отклонение от горизонтального положения образующей конуса относительно плиты, на которой находится С. л. С помощью С. л. обычно устанавливают углы от 0 до 45° с погрешностью от 4 до 15'', зависящей от номинального расстояния между роликами, от размера угла, на который производится установка С. л., и от точности её изготовления.
Принцип С. л. используется, например, в конструкциях различных приборов для передачи движений под углом к основному движению, в приспособлениях к металлорежущим станкам при обработке деталей с наклонными поверхностями.
Лит.: Эйдинов В. Я., Измерение углов в машиностроении, М., 1963; Конические соединения, М., 1968.
Н. Н. Марков.
Измерение угла при использовании синусной линейки: а — наружного конуса; б — внутреннего конуса; 1 — конусный калибр; 2 — отсчётная головка; I и II — положения отсчётной головки.
Синусов теорема
Си'нусов теоре'ма,теорема тригонометрии, устанавливающая соотношения между сторонами а, Ь, с произвольного треугольника и синусами противолежащих им углов А, В, С. Содержание С. т. заключается в равенствах:
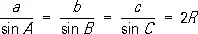
где R — радиус описанного круга.
Синусов условие
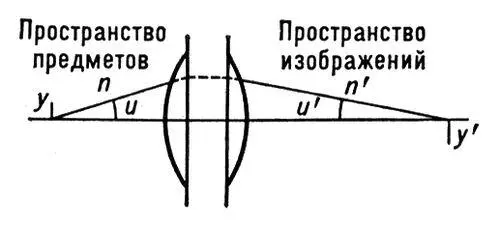
Си'нусов усло'виев оптике должно соблюдаться, чтобы оптическая система, исправленная в отношении сферической аберрации, давала неискажённое (безаберрационное) изображение y' малого линейного элемента у, расположенного на оптической оси системы и перпендикулярного этой оси ( рис. ). С. у. выражается формулой sinu/sin u' = b n'/n, где u и u' — углы, образуемые с оптической осью лучом, проходящим через находящиеся на оси точки предмета и соответственно его изображения; n и n' — преломления показатели сред по обе стороны оптической системы; b = у'/у — линейное увеличение оптическое системы.
Рис. к ст. Синусов условие.
Синусоида
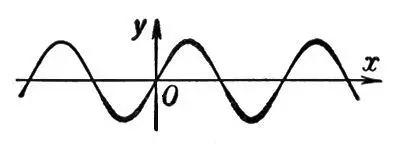
Синусо'ида,график функции у= sin x', плоская кривая (см. рис. ), изображающая изменение синуса в зависимости от изменения его аргумента (угла). С. пересекает ось Ox в точках 180 ° k (или p k ) ', в точках вида 90°+360% (или p/2 + 2pk) имеет максимумы, а в точках —90° + 360 ° k (или — p/2 + 2p k ) — минимумы ( k = 0, ± 1,...). Часто С. называют кривую, определяемую уравнением у = A sin (wx- + j 0), которая получается из кривой у = sin х растяжением (в w раз) по оси Ox, растяжением (в А раз) по оси Оу и сдвигом (на —j 0/w). Число А называется амплитудой, w — круговой частотой, j 0— начальной фазой. С. имеет большое значение в теории колебаний.
Рис. к. ст. Синусоида.
Синусоидальные колебания
Синусоида'льные колеба'ния,колебания, при которых изменения колеблющейся величины происходят по синусоиде, то же, что гармонические колебания.
Синусоидальные спирали
Синусоида'льные спира'ли,синус-спирали, кривые, уравнения которых в полярной системе координат имеют вид
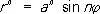 , (*)
, (*)
где n — рациональное число. Частными случаями С. с. являются окружность, прямая, равнобочная гипербола, лемниската, кардиоида, парабола (см. Линия )
(соответственно при n = 1, —1, —2, 2,
 ,
, 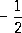 ). Логарифмическую спираль можно рассматривать как некоторый предельный случай С. с. при n = 0 [хотя уравнение (*) теряет при этом смысл], разделяющей С. с., лежащие в конечной части плоскости, от С. с., имеющих бесконечные ветви. Проекция центра кривизны любой точки С. с. на радиус-вектор этой точки делит его в отношении n: 1 (считая от полюса). При равномерном вращении радиус-вектора С. с. вокруг полюса касательная равномерно вращается вокруг точки касания. Поэтому С. с. называются также кривыми пропорционального изгиба. При натуральном n С. с. состоит из n лепестков, лежащих в углах
). Логарифмическую спираль можно рассматривать как некоторый предельный случай С. с. при n = 0 [хотя уравнение (*) теряет при этом смысл], разделяющей С. с., лежащие в конечной части плоскости, от С. с., имеющих бесконечные ветви. Проекция центра кривизны любой точки С. с. на радиус-вектор этой точки делит его в отношении n: 1 (считая от полюса). При равномерном вращении радиус-вектора С. с. вокруг полюса касательная равномерно вращается вокруг точки касания. Поэтому С. с. называются также кривыми пропорционального изгиба. При натуральном n С. с. состоит из n лепестков, лежащих в углах
 ,
, 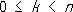
касаясь в начале координат сторон угла. Углы
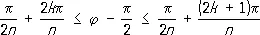 ,
, 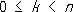
Интервал:
Закладка: