БСЭ БСЭ - Большая Советская Энциклопедия (СИ)

Структурная С. биосистем изучается также с точки зрения более общих типов С. — цветной С., С. подобия, антисимметрии и др.

Разработка учения о С. биообъектов позволит углубить представления как об их свойствах и функциях, так и о происхождении и сущности жизни .

Лит.: Гаузе Г. Ф., Асимметрия протоплазмы, М. — Л., 1940; Вайнштейн Б. К., Дифракция рентгеновых лучей на цепных молекулах, М., 1963; Беклемишев В. Н., Основы сравнительной анатомии беспозвоночных, 3 изд., т. 1—2, М., 1964; Урманцев Ю. А., Симметрия природы и природа симметрии, М., 1974; Ludwig W., Das Rechts-Links-Problem im Tierreich und beim Menschen..., B. — Hdib. — N. Y., 1970; Bentley R., Molecular asymmetry in biology, v. 1—2, N. Y., 1969—70.

Ю. А. Урманцев.

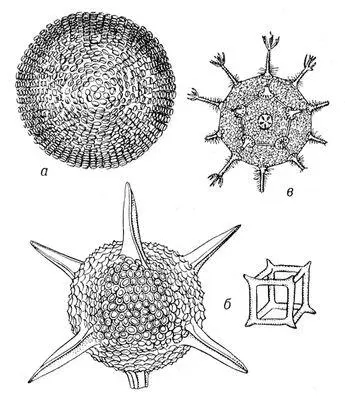
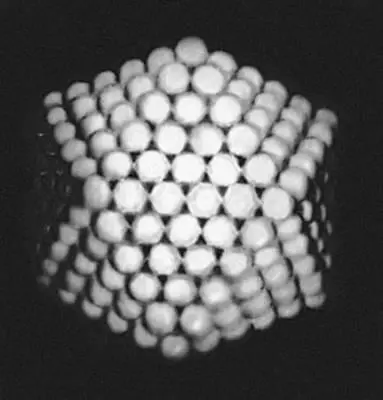
Рис. 3. Биообъекты с совершенной точечной симметрией. Радиолярии: а — шарообразная Ethmosphaera polysyphonia, содержащая бесконечное число осей бесконечного порядка + бесконечное число плоскостей симметрии + центр симметрии; б — кубические Hexastylus marginatus и Lithocubus geometricus, характеризующиеся симметрией куба; в — додекаэдрическая Circorhegma dodecahedra, характеризующаяся симметрией правильных многогранников — додекаэдра и икосаэдра.

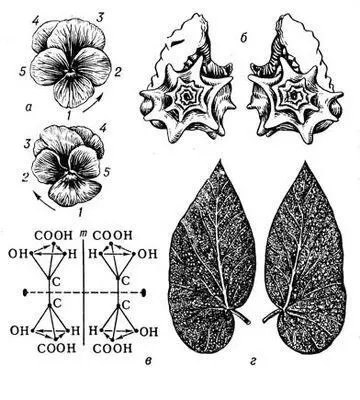
Рис. 4. Диссимметрические D- и L-биообъекты: а — цветки анютиных глазок; б — раковины прудовика; в — молекулы винной кислоты; г — листья бегонии.

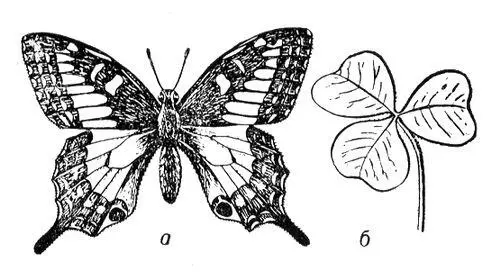
Рис. 2. Актиноморфная симметрия; а — бабочка; б — лист кислицы; симметрии соответственно 1×m, 3×m. Бабочке свойственна двусторонняя, или билатеральная, симметрия.

Рис. 5. Лист липы, иллюстрирующий возможность существования диссимметрических объектов более чем в двух (в данном случае в 16) модификациях. Для листа липы диссфакторы — это 4 морфологических признака: преимущественные ширина (ш) и длина (д), асимметричные жилкование (ж) и загиб главной жилки (г). Так как каждый из диссфакторов может проявляться двояко — в (+)- или ( — )-формах — и соответственно приводить к D- или L-мoдификациям, то число возможных модификаций будет 2 4= 16, а не две.

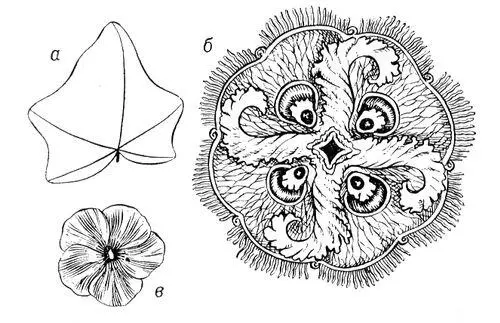
Рис. 1. Аксиальная симметрия: а — лист плюща; б — медуза Aurelia insulinda; в — цветок флокса. При повороте этих фигур вокруг оси симметрии равные части каждого из них совпадут друг с другом соответственно 1, 4, 5 раз (оси 1, 4, 5-го порядка). Лист плюща асимметричен.

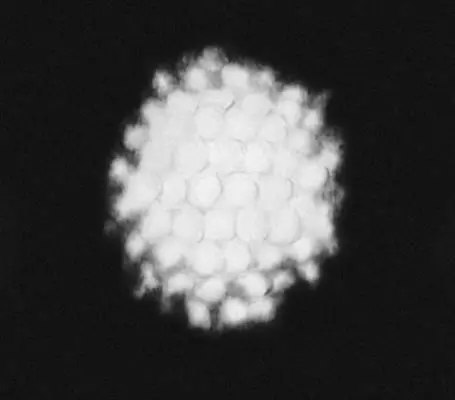
Рис. 3д. Биообъекты с совершенной точечной симметрией. Радиолярии: модель аденовируса в форме икосаэдра.

Рис. 3г. Биообъекты с совершенной точечной симметрией. Радиолярии: частица аденовируса в форме икосаэдра.

Симме'трия(от греч. symmetria — соразмерность) в математике,

1) симметрия (в узком смысле), или отражение (зеркальное) относительно плоскости a в пространстве (относительно прямой а на плоскости), — преобразование пространства (плоскости), при котором каждая точка М переходит в точку M' такую, что отрезок MM' перпендикулярен плоскости a (прямой а ) и делится ею пополам. Плоскость a (прямая а ) называется плоскостью (осью) С.

Отражение — пример ортогонального преобразования , изменяющего ориентацию (в отличие от собственного движения). Любое ортогональное преобразование можно осуществить последовательным выполнением конечного числа отражений — этот факт играет существенную роль в исследовании С. геометрических фигур.

2) Симметрия (в широком смысле) — свойство геометрической фигуры Ф , характеризующее некоторую правильность формы Ф , неизменность её при действии движений и отражений. Точнее, фигура Ф обладает С. (симметрична), если существует нетождественное ортогональное преобразование, переводящее эту фигуру в себя. Совокупность всех ортогональных преобразований, совмещающих фигуру Ф с самой собой, является группой , называемой группой симметрии этой фигуры (иногда сами эти преобразования называются симметриями).

Так, плоская фигура, преобразующаяся в себя при отражении, симметрична относительно прямой — оси С. ( рис. 1 ); здесь группа симметрии состоит из двух элементов. Если фигура Ф на плоскости такова, что повороты относительно какой-либо точки О на угол 360°/ n , n — целое число ³ 2, переводят её в себя, то Ф обладает С. n -го порядка относительно точки О — центра С. Примером таких фигур являются правильные многоугольники ( рис. 2 ); группа С. здесь — т. н. циклическая группа n -го порядка. Окружность обладает С. бесконечного порядка (поскольку совмещается с собой поворотом на любой угол).

Простейшими видами пространственной С., помимо С., порожденной отражениями, являются центральная С., осевая С. и С. переноса.

а) В случае центральной симметрии (инверсии) относительно точки О фигура Ф совмещается сама с собой после последовательных отражений от трёх взаимно перпендикулярных плоскостей, другими словами, точка О — середина отрезка, соединяющего симметричные точки Ф ( рис. 3 ). б) В случае осевой симметрии, или С. относительно прямой n -го порядка, фигура накладывается на себя вращением вокруг некоторой прямой (оси С.) на угол 360°/ n . Например, куб имеет прямую AB осью С. третьего порядка, а прямую CD — осью С. четвёртого порядка ( рис. 3 ); вообще, правильные и полуправильные многогранники симметричны относительно ряда прямых. Расположение, количество и порядок осей С. играют важную роль в кристаллографии (см. Симметрия кристаллов ), в) Фигура, накладывающаяся на себя последовательным вращением на угол 360°/2 k вокруг прямой AB и отражением в плоскости, перпендикулярной к ней, имеет зеркально-осевую С. Прямая AB , называется зеркально-поворотной осью С. порядка 2 k , является осью С. порядка k ( рис. 4 ). Зеркально-осевая С. порядка 2 равносильна центральной С. г) В случае симметрии переноса фигура накладывается на себя переносом вдоль некоторой прямой (оси переноса) на какой-либо отрезок. Например, фигура с единственной осью переноса обладает бесконечным множеством плоскостей С. (поскольку любой перенос можно осуществить двумя последовательными отражениями от плоскостей, перпендикулярных оси переноса) ( рис. 5 ). Фигуры, имеющие несколько осей переноса, играют важную роль при исследовании кристаллических решёток .