БСЭ БСЭ - Большая Советская Энциклопедия (СИ)

Лит.: Айзенберг Г. З., Антенны ультракоротких воля, [ч. 1], М., 1957; Лавров Г. А., Князев А. С., Приземные и подземные антенны, М., 1965; Драбкин А. Л., 3узенко В. Л., Кислов А. Г., Антенно-фидерные устройства, 2 изд., М., 1974.

Г. А. Клигер, В. И. Комиссаров.

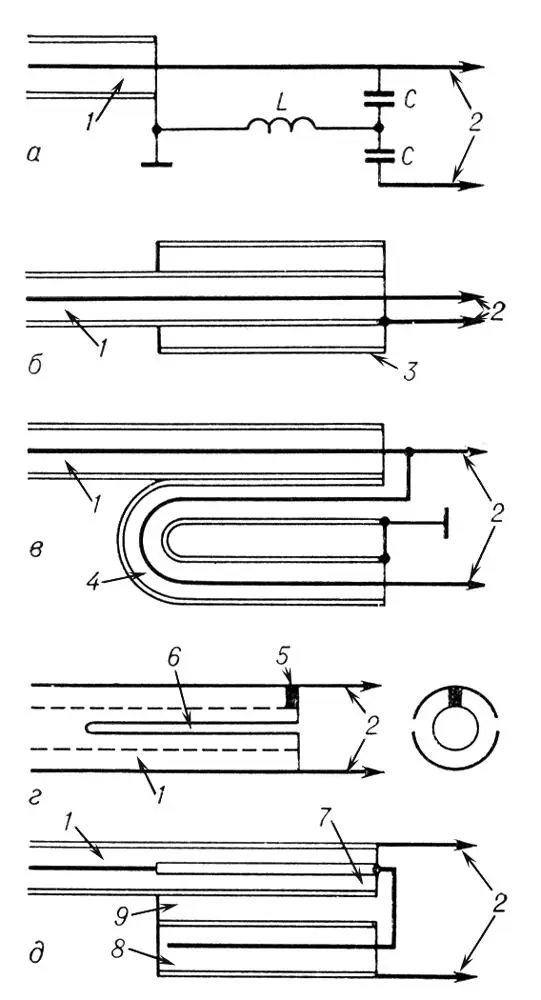
Симметрирующие устройства: а — однозвенное; б — «четвертьволновой стакан»; в — «U-колено»; г — коаксиально-щелевой переход; д — устройство с компенсацией рассогласования; 1 — несимметричная линия; 2 — симметричная линия; 3 — «стакан»; 4 — полуволновая петля; 5 — проводящая перемычка; 6 — щель; 7 — коаксиальный трансформатор; 8 — компенсирующий разомкнутый шлейф; 9 — симметрирующий короткозамкнутый шлейф; L — катушка индуктивности; С — конденсатор.

Симметри'ческая гру'ппаn-й степени, группа , состоящая из всех перестановок n объектов. В С. г. n ! элементов. Перестановки С. г. с чётным числом инверсии образуют знакопеременную, или полусимметрическую, подгруппу С. г., имеющую n !/2 элементов.

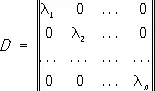
Симметри'ческая ма'трица,квадратная матрица S = ll s ik ll, в которой любые два элемента, симметрично расположенные относительно главной диагонали, равны между собой: s ik = s ki ( i , k = 1,2,..., n ). С. м. часто рассматривается как матрица коэффициентов некоторой квадратичной формы ; между теорией С. м. и теорией квадратичных форм существует тесная связь.

Спектральные свойства С. м. с действительными элементами: 1) все корни l 1, l 2,..., l n характеристического уравнения С. м. действительны; 2) этим корням соответствуют n попарно ортогональных собственных векторов С. м. ( n — порядок С. м.). С. м. с действительными элементами всегда представима в виде: S'= ODO -1

где О ортогональная матрица , а

.

Симметри'ческие фу'нкции,функции нескольких переменных, не изменяющиеся при любых перестановках переменных, например 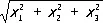или 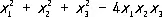. Особое значение в алгебре имеют симметрические многочлены (с. м.) и среди них — элементарные симметрические многочлены (э. с. м.) — функции

, , , …, ,

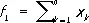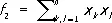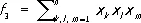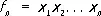где суммы распространены на комбинации неравных между собой чисел k , l ,...; они имеют первую степень относительно каждого из переменных. Согласно формулам Виета, x 1 , x 2 ,..., x n являются корнями уравнения:

x n- f 1x n-1+ f 2x n-2- ··· + (- 1 ) nf n = 0.

Согласно основной теореме теории С. ф., любой с. м. представляется как многочлен от э. с. м., и притом только единственным образом: F ( x 1 , x 2. , ... , x n ) = G ( f 1 , f 2 ,..., f n ); если все коэффициенты в F целые, то и коэффициенты в G целые. Иными словами, всякий с. м. от корней уравнения выражается целым рациональным образом через его коэффициенты; например,

.

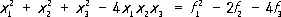Другим важным классом С. ф. являются степенные суммы

.

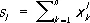Они связаны с э. с. м. формулами Ньютона

s i- f 1s l-1+ f 2s l-2 + ··· + (— 1) l f l = 0, ,

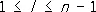и

s n+l - f 1s n+l-1 + ··· +(-1) n f ns l= 0,

,

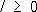позволяющими последовательно выражать f k через s rn и обратно.

Функция называется кососимметрической, или знакопеременной, если она не изменяется при чётных перестановках x 1 , x 2 , ... , x n и меняет знак при нечётных перестановках. Такие функции рационально выражаются через f 1 , f 2 , ... , f n и разностное произведение (см. Дискриминант ) D = П к<1 ( x k — x l ), квадрат которого является С. ф. и потому рационально выражается через f 1 , f 2 ,..., f n.

Лит.: Курош А. Г., Курс высшей алгебры, 10 изд., М., 1971.

Симметри'чностьв математике и логике, свойство бинарных (двуместных, двучленных) отношений , выражающее независимость выполнимости данного отношения для какой-либо пары объектов от порядка, в котором эти объекты входят в пару: отношение R называется симметричным, если для любых объектов x и y из области определения xRy влечёт yRx . Примерами симметричных отношений служат отношения типа равенства ( тождества , эквивалентности , подобия ), их «ослабленные формы» — отношения толерантности (сходства, соседства и т. п.), а также (как следует из данного выше определения) обратные к ним отношения неравенства и др. Отношение R называется антисимметричным, если из xRy при х ( у следует ù yRx (отрицание yRx ), т. е. если из xRy и yRx непременно следует х = у , таковы, например, отношения порядка (по величине или какому-либо другому упорядочивающему критерию) между числами или другими объектами, отношение включения между множествами и т. п. В применении к логическим и логико-математическим операциям свойство С. называется коммутативностью (перестановочностью); например, результаты сложения и умножения чисел, объединения и пересечения множеств, дизъюнкция и конъюнкция высказываний (см. Алгебра логики ) не зависят от порядка слагаемых, сомножителей и т. д. Понятия С. и коммутативности естественно обобщаются на случай произвольного числа объектов.

Симметри'яв биологии (биосимметрия). На явление С. в живой природе обратили внимание ещё в Древней Греции пифагорейцы (5 в. до н. э.) в связи с развитием ими учения о гармонии. В 19 в. появились единичные работы, посвященные С. растений (французские учёные О. П. Декандоль, О. Браво), животных (немецкий — Э. Геккель), биогенных молекул (французские — А. Вешан, Л. Пастер и др.). В 20 в. биообъекты изучали с позиций общей теории С. (советские учёные Ю. В. Вульф, В. Н. Беклемишев, Б. К. Вайнштейн, голландский физикохимик Ф. М. Егер, английский кристаллографы во главе с Дж. Берналом) и учения о правизне и левизне (советские учёные В. И. Вернадский, В. В. Алпатов, Г. Ф. Гаузе и др.; немецкий учёный В. Людвиг). Эти работы привели к выделению в 1961 особого направления в учении о С. — биосимметрики.