БСЭ БСЭ - Большая Советская Энциклопедия (СИ)

Группы симметрии классифицируют: по числу n измерений пространства, в которых они определены; по числу т измерений пространства, в которых объект периодичен (их соответственно обозначают G m n ) и по некоторым другим признакам. Для описания кристаллов используют различные группы симметрии, из которых важнейшими являются пространственные группы симметрии G 3 3 , описывающие атомную структуру кристаллов, и точечные группы симметрии G 0 3 , описывающие их внешнюю форму. Последние называются также кристаллографическими классами.

Симметрия огранки кристаллов.Операциями точечной симметрии являются: повороты вокруг оси симметрии порядка N на 360°/ N ( рис. 2 , а), отражение в плоскости симметрии (зеркальное отражение, рис. 2 , б), инверсия 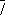(симметрия относительно точки, рис. 2 , в), инверсионные повороты 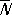(комбинация поворота на 360°/ N с одновременной инверсией, рис. 2 , г). Вместо инверсионных поворотов иногда рассматривают зеркальные повороты 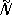. Геометрически возможные сочетания этих операций определяют ту или иную точечную группу ( рис. 3 ), которые изображаются обычно в стереографической проекции. При преобразованиях точечной симметрии по крайней мере одна точка объекта остаётся неподвижной — преобразуется сама в себя. В ней пересекаются все элементы симметрии, и она является центром стереографической проекции.

Точечные преобразования симметрии g [ x 1, x 2, x 3] = 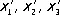описываются линейными уравнениями:

x' 1= а 11 х 1+ a 12 x 2+ a 13 x 3,

x' 2= a 21 x 1+ a 22 x 2+ a 23 x 3, (2)

x' 3= a 31 x 1+ a 32 x 2+ a 33 x 3,

т. е. матрицей коэффициента ( a ij). Например, при повороте вокруг хз на угол a = 360°/ N матрица коэффициентов имеет вид:

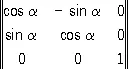, (3)

а при отражении в плоскости x 1, x 2имеет вид:

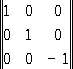(3a)

Поскольку N может быть любым, число групп 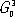бесконечно. Однако в кристаллах ввиду наличия кристаллической решётки возможны только операции и соответственно оси симметрии до 6-го порядка (кроме 5-го), которые обозначаются символами: 1 , 2 , 3 , 4 , 6 , а также инверсионные оси: 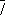(она же центр симметрии), 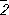= m (она же плоскость симметрии), 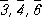. Поэтому количество точечных кристаллографических групп, описывающих внешнюю форму кристаллов, ограничено. Эти 32 группы С. к. приведены в таблице. В международные обозначения точечных групп входят символы основных (порождающих) элементов симметрии, им присущих. Эти группы объединяются по симметрии формы элементарной ячейки (с периодами а , b , с и углами a, b, g) в 7 сингоний кристаллографических — триклинную, моноклинную, ромбическую, тетрагональную, тригональную, гексагональную и кубическую. Принадлежность кристалла к той или иной группе определяется гониометрически (см. Гониометр ) или рентгенографически (см. Рентгеновский структурный анализ ).

Группы, содержащие лишь повороты, описывают кристаллы, состоящие только из совместимо равных частей. Эти группы называются группами 1-го рода. Группы, содержащие отражения, или инверсионные повороты, описывают кристаллы, в которых есть зеркально равные части (но могут быть и совместимо равные части). Эти группы называются группами 2-го рода. Кристаллы, описываемые группами 1-го рода, могут кристаллизоваться в двух энантиоморфных формах, условно называемых «правой» и «левой», каждая из них не содержит элементов симметрии 2-го рода, но они зеркально равны друг другу (см. Энантиоморфизм , Кварц ).

Точечные группы описывают симметрию не только кристаллов, но любых конечных фигур. В живой природе часто наблюдается запрещенная в кристаллографии симметрия с осями 5-го, 7-го порядка и выше. Например, для описания регулярной структуры сферических вирусов ( рис. 4 ), в оболочках которых соблюдаются кристаллографические принципы плотной укладки молекул, оказалась важной икосаэдрическая точечная группа 532.

Симметрия физических свойств. Предельные группы.В отношении макроскопических физических свойств (оптических, электрических, механических и др.), кристаллы ведут себя как однородная анизотропная среда, т. е. дискретность их атомной структуры не проявляется. Однородность означает, что свойства одинаковы в любой точке кристалла, однако при этом многие свойства зависят от направления (см. Анизотропия ). Зависимость от направления можно представить в виде функции и построить указательную поверхность данного свойства ( рис. 5, см. также ст. Кристаллооптика ). Эта функция, которая может быть различной для разных физических свойств кристалла (векторной или тензорной) имеет определённую точечную симметрию, однозначно связанную с группой симметрии огранения кристалла. Она либо совпадает с ней, либо выше её по симметрии (принцип Неймана).

Многие из свойств кристаллов, принадлежащих к определённым классам, описываются предельными точечными группами, содержащими оси симметрии бесконечного порядка, обозначаемые ¥. Наличие оси ¥ означает, что объект совмещается с собой при повороте на любой, в том числе бесконечно малый угол. Таких групп 7, они представлены на рис. 6 образцовыми фигурами и соответствующими символами. Т. о., всего имеется 32 + 7 = 39 точечных групп, описывающих симметрию свойств кристаллов. Зная группу С. к., можно указать возможность наличия или отсутствия в нём некоторых физических свойств (см. Кристаллы , Кристаллофизика ).

Обозначения и названия 32 групп точечной симметрии

Сингония	Обозначения	Название	Соотношение констант эле - ментарной ячейки
международные	по Шенфлису
Триклинная		С 1	Моноэдрическая	а ¹ b ¹ с
	С 1	Пинакоидальная	a ¹ b ¹ g ¹ 90°
Моноклинная	2	С 2	Диэдрическая осевая	а ¹ b ¹ с
m	Cs	Диэдрическая безосная	a = g = 90°
2/m	C 2h	Призматическая	b ¹ 90°
Ромбическая	222	D 2	Ромбо-тетраэдрическая	а ¹ b ¹ с
mm	C 2 u	Ромбо-пирамидальная
mmm	D 2h	Ромбо-дипирамидальная	a = b = g = 90°
Тетрагональная	4	C 4	Тетрагонально-пирамидальная	а = b ¹ с a = b = g = 90°
422	D 4	Тетрагонально-трапецоэдрическая
4/m	C 4h	Тетрагонально-дипирамидальная
4mm	C 4 u	Дитетрагонально-пирамидальная
4/mmm	D 4h	Дитетрагонально-дипирамидальная
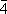	S 4	Тетрагонально-тетраэдрическая
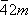	D 2d	Тетрагонально-скаленоэдрическая
Тригональная	3	C 3	Тригонально-пирамидальная	а = b = с a = b = g ¹ 90°
32	D 3	Тригонально-трапецоэдрическая
3m	C 3 u	Дитригонально-пирамидальная
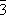	C 3i	Ромбоэдрическая
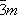	D 3d	Дитригонально-скаленоэдрическая
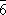	C 3h	Тригонально-дипирамидальная
Гексагональная		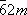D 3h	Дитригонально-дипирамидальная	а = b ¹ с a = b = 90° g = 120°
6	C 6	Гексагонально-пирамидальная
62	D 6	Гексагонально-трапецоэдрическая
6/m	C 6h	Гексагонально-дипирамидальная
6mm	C 6 u	Дигексагонально-пирамидальная
6/mmm	D 6h	Дигексагонально-дипирамидальная
Кубическая	23	T	Тритетраэдрическая	а = b = с a = b = g = 90°
m3	T h	Дидодекаэдрическая
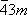	T d	Гексатетраэдрическая
43	O	Триоктаэдрическая
m3m	Oh	Гексоктаэдрическая

Пространственная симметрия атомной структуры кристаллов(кристаллической решётки) описывается пространственными группами симметрии 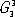. Характерными для решётки операциями являются три некомпланарных переноса а , b , с , называемых трансляциями, которые задают трёхмерную периодичность атомной структуры кристаллов. Сдвиг (перенос) структуры на векторы a 1 , b 2 , c 3 или любой вектор t = p 1a 1 + p 2b 2 + p 3c 3 , где p 1 , p 2 , p 3 — любые целые положительные или отрицательные числа, совмещает структуру кристалла с собой, и следовательно, является операцией симметрии, удовлетворяющей условиям ( 1 , а, б). Параллелепипед, построенный на векторах а , b и c , называется параллелепипедом повторяемости или элементарной ячейкой кристалла ( рис. 7 , а, б). В элементарной ячейке содержится некоторая минимальная группировка атомов, «размножение» которой операциями симметрии, в том числе трансляциями, образует кристаллическую решётку. Элементарная ячейка и размещение в ней атомов устанавливается методами рентгеновского структурного анализа , электронографии или нейтронографии .