БСЭ БСЭ - Большая Советская Энциклопедия (СИ)

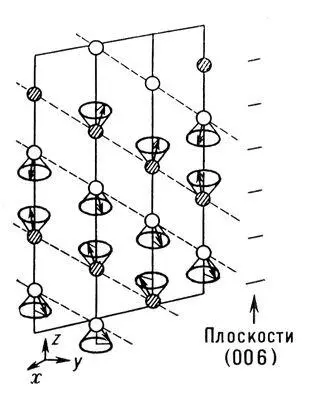
Вследствие возможности комбинирования в решётке трансляций и операций точечной симметрии в группах G 3 3 возникают операции и соответствующие им элементы симметрии с трансляционной компонентой — винтовые оси различных порядков и плоскости скользящего отражения ( рис. 2 , д).

Всего известно 230 пространственных (фёдоровских) групп симметрии 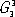, и любой кристалл относится к одной из этих групп. Трансляционные компоненты элементов микросимметрии макроскопически не проявляются, например винтовая ось в огранке кристаллов проявляется как соответствующая по порядку простая поворотная ось. Поэтому каждая из 230 групп 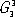макроскопически сходственна с одной из 32 точечных групп. Например, точечной группе mmm или D 2h сходственны 28 пространственных групп. Совокупность переносов, присущих данной пространственной группе, есть её трансляционная подгруппа, или Браве решётка ; таких решёток существует 14.

Симметрия слоев и цепей.Для описания плоских или вытянутых в одном направлении фрагментов структуры кристаллов могут быть использованы группы 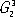— двумерно периодические и 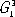— одномерно периодические в трёхмерном пространстве. Эти группы играют важную роль в изучении биологических структур и молекул. Например, группы 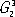описывают строение биологических мембран , группы 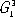— цепных молекул ( рис. 8 , а) палочкообразных вирусов , трубчатых кристаллов глобулярных белков ( рис. 8 , б), в которых молекулы уложены согласно спиральной (винтовой) симметрии, возможной в группах .

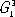Обобщённая симметрия.В основе определения симметрии лежит понятие равенства ( 1 , б) при преобразовании ( 1 , а). Однако физически (и математически) объект может быть равен себе по одним признакам и не равен по другим. Например, распределение ядер и электронов в кристалле антиферромагнетика можно описать с помощью обычной пространственной симметрии, но если учесть распределение в нём магнитных моментов ( рис. 9 ), то «обычной», классической симметрии уже недостаточно. К подобного рода обобщениям симметрии относится антисимметрия и цветная симметрия. В антисимметрии в дополнение к трём пространственным переменным x 1 , x 2 , x 3 вводится добавочная, 4-я переменная x 4 = ± 1. Это можно истолковать таким образом, что при преобразовании ( 1 , а) функция F может быть не только равна себе, как в ( 1 , б), но и изменить знак. Условно такую операцию можно изобразить изменением цвета ( рис. 10 ). Существует 58 групп точечной антисимметрии 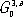и 1651 пространственная группа антисимметрии 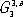(шубниковских групп). Если добавочная переменная приобретает не два значения, а несколько (возможны числа 3, 4, 6, 8,..., 48), то возникает «цветная» симметрия Белова. Так, известна 81 точечная группа G 0 3, ц . Основные приложения обобщённой симметрии в кристаллографии — описание магнитных структур.

Др. обобщения симметрии: симметрия подобия, когда равенство частей фигуры заменяется их подобием ( рис. 11 ), криволинейная симметрия, статистическая симметрия, вводимая при описании структуры разупорядоченных кристаллов, твёрдых растворов , жидких кристаллов , и др.

Лит.: Шубников А. В., Копцик В. А., Симметрия в науке и искусстве, 2 изд., М., 1972; Вейль Г., Симметрия, пер. с англ., М., 1968; Федоров Е. С.. Симметрия и структура кристаллов, [М.], 1949; Шубников А. В., Симметрия и антисимметрия конечных фигур, М., 1951.

Б. К. Вайнштейн.

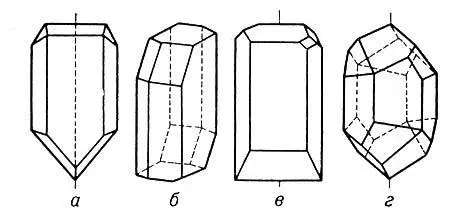
Рис. 3. Примеры кристаллов, принадлежащих к разным точечным группам или кристаллографическим классам: а — к классу m (одна плоскость симметрии); б — к классу с (один центр симметрии); в — к классу 2 (одна ось симметрии 2-го порядка); г — к классу 6 (одна зеркальная ось 6-го порядка).

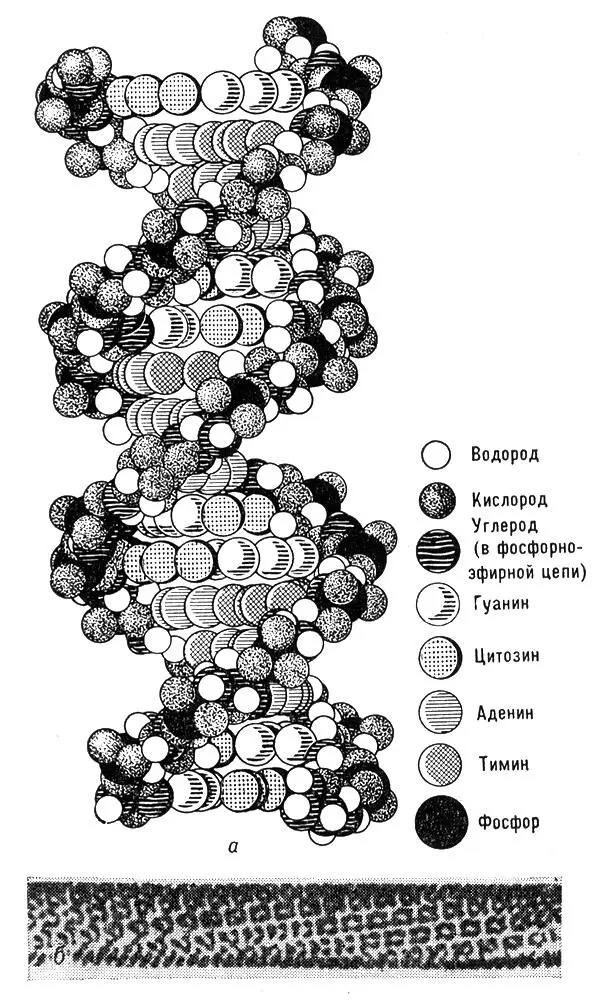
Рис. 8. Объекты со спиральной симметрией: а — молекула ДНК; б — трубчатый кристалл белка фосфорилазы (электронномикроскопический снимок, увеличено).

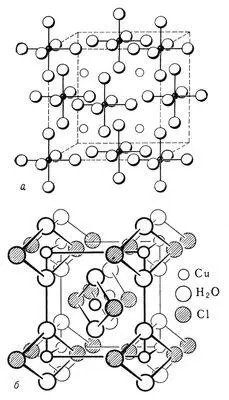
Рис. 7. Элементарные ячейки кристаллов: а — K 2PtCl 6; б — CuCl 2×2H 2O.

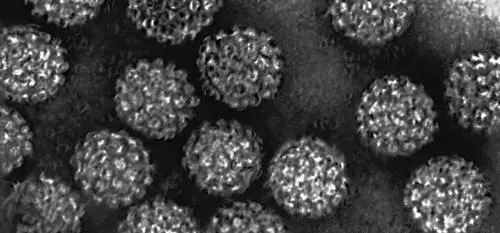
Рис. 4. Cферический вирус (электронно-микроскопический снимок, увеличено).

Рис. 9. Распределение магнитных моментов (стрелки) в элементарной ячейке кристалла Cr 2O 3.

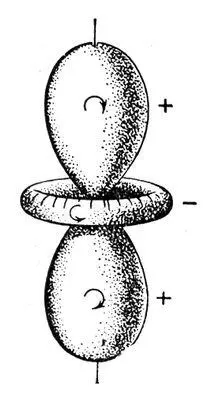
Рис. 5. Поверхность, описывающая оптическую активность кристалла кварца; знаки (+) и (-) указывают противоположные направления вращения плоскости поляризации.

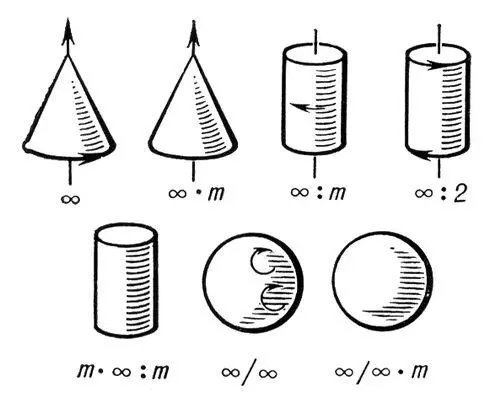
Рис. 6. Фигуры, иллюстрирующие предельные группы симметрии.

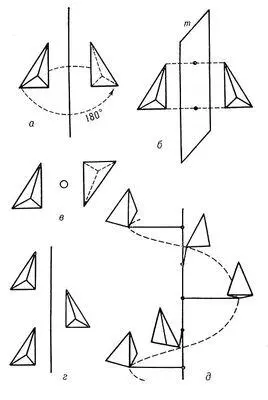
Рис. 2. Простейшие операции симметрии: а — поворот; б — отражение; в — инверсия; г — скользящее отражение; д — винтовой поворот 4-го порядка.

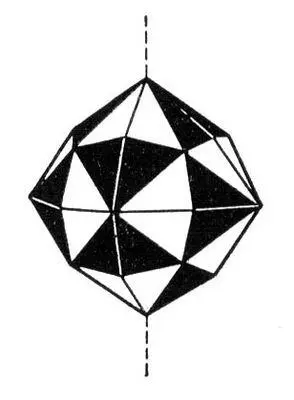
Рис. 10. Фигура, описываемая точечной группой антисимметрии.

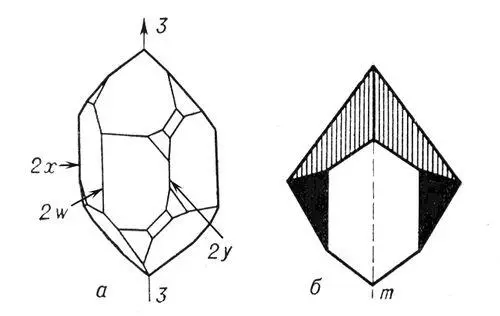
Рис. 1. а — кристалл кварца: 3 — ось симметрии 3-го порядка, 2x ,2y, 2w — оси второго порядка; б — кристалл водного метасиликата натрия: m — плоскость симметрии.

Рис. 11. Фигура, обладающая симметрией подобия.