БСЭ БСЭ - Большая Советская Энциклопедия (СО)

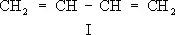
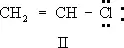
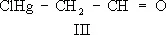
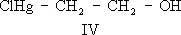
Общая особенность всех сопряжённых систем — «растекание» электронной плотности р- и p-электронов (см. Сигма- и пи-связи ) по всей сопряжённой системе — определяет их физические и химические свойства. Так, простые связи приобретают некоторую «двоесвязность», выражающуюся, в частности, в уменьшении их длины. Например, в бутадиене длина центральной С — С-связи 1,46 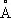вместо обычной 1,54 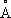. С. с. проявляется также, например, в УФ- и ИК-спектрах, дипольных моментах. Наиболее характерная химическая особенность сопряжённых систем — способность вступать в реакции не только с участием одной кратной связи, но и всей сопряжённой системы как единого целого. Примером может служить, например, присоединение к бутадиену хлористого водорода:

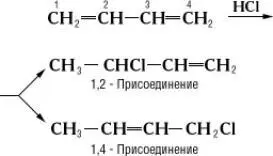
Количество образующихся продуктов 1,2-и 1,4-присоединения зависит от природы сопряжённой системы, от реагента и условий реакции. Сопряжение снижает внутреннюю энергию молекул и, следовательно, делает их более устойчивыми: величина энергии сопряжения колеблется между несколькими единицами и десятками ккал/моль (например, для бутадиена 3,6 ккал/моль, для бензола 35 ккал/моль, 1 ккал/моль =4,19 кдж/моль ) .

Истинное распределение электронной плотности в сопряжённых системах нельзя выразить простейшими структурными формулами. Их строение более точно передаётся наборами предельных структур (см. Мезомерия, Резонанса теория ) , формулами с пунктирными («полуторными») связями или с изогнутыми стрелками, указывающими направление сдвига электронов, например:

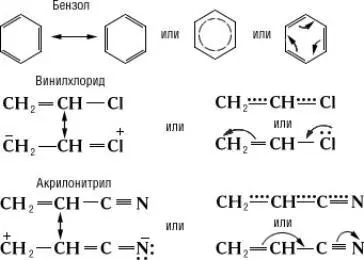
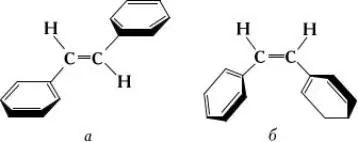
Для проявления С. с. необходимо, чтобы участвующие в нём электронные системы находились в одной плоскости. Если структура молекулы не допускает этого, то говорят о пространственных препятствиях сопряжению. Так, у транс- стильбена (а), по данным УФ-спектров, обнаруживается более сильное сопряжение, чем у цис- стильбена (б), у которого бензольные ядра не могут разместиться в одной плоскости с двойной связью:

Сопряжённые гипе'рболы,две гиперболы, которые в одной и той же системе прямоугольных координат при одних и тех же значениях а и b определяются уравнениями:

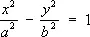
и

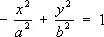
С. г. имеют общие асимптоты и общий основной прямоугольник (см. рис.).

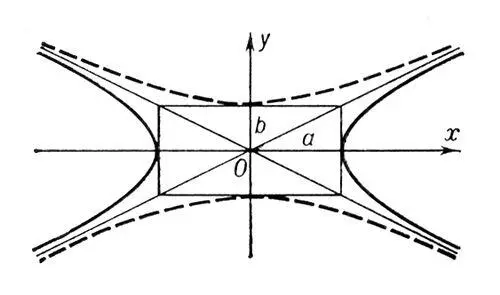
Рис. к ст. Сопряжённые гиперболы.

Сопряжённые диа'метрылинии второго порядка, два диаметра, каждый из которых делит пополам хорды этой кривой, параллельные другому. С. д. играют важную роль в общей теории линий второго порядка. При параллельном проектировании эллипса в окружность его С. д. проектируются в пару взаимно перпендикулярных диаметров окружности.

Сопряжённые дифференциа'льные уравне'ния,понятие теории дифференциальных уравнений. Уравнением, сопряжённым с дифференциальным уравнением

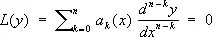, (1)

называется уравнение

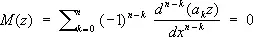, (2)

Соотношение сопряженности взаимно. Для С. д. у. имеет место тождество

,

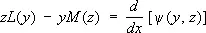где y ( у, z ) — билинейная форма относительно у, z и их производных до ( n - 1)-го порядка включительно. Знание k интегралов сопряжённого уравнения позволяет понизить на k единиц порядок данного уравнения. Если

y 1, у 2,... у n (3)

— фундаментальная система решений уравнения (1), то фундаментальная система решений уравнения (2) даётся формулами

,

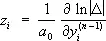
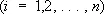где D — определитель Вроньского (см. Вронскиан ) системы (3). Если для уравнения (1) заданы краевые условия, то существуют сопряжённые с ними краевые условия для уравнения (2) такие, что уравнения (1) и (2) с соответствующими краевыми условиями определяют сопряжённые дифференциальные операторы (см. Сопряжённые операторы ) . Понятие сопряженности обобщается также на системы дифференциальных уравнений и на уравнения с частными производными.

Сопряжённые опера'торы,понятие операторов теории. Два ограниченных линейных оператора Т и Т* в гильбертовом пространстве называются сопряжёнными, если для всех векторов х и у из Н справедливо соотношение ( Tx, у ) = ( х, Т*у ) . Например, если

,

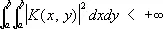то оператору

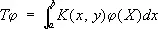
сопряжён оператор

,

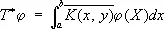где 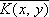— функция, комплексно сопряжённая с К ( х, у ) . Если оператор Т не ограничен и его область определения D m всюду плотна (см. Плотные и неплотные множества ) , то С. о. определяется на множестве тех векторов у, для которых можно найти такой вектор у*, что равенство ( Tx, у ) = ( х, у* ) справедливо для всех х Î D m, при этом полагают Т*у = у*. Понятие сопряженности обобщается также на операторы в др. пространствах.