БСЭ БСЭ - Большая Советская Энциклопедия (ТЕ)

В формулировке Т. различают условие и заключение. Например, 1) если сумма цифр числа делится на 3, то и само число делится на 3, или 2) если в треугольнике один из углов прямой, то оба других — острые; в каждом из этих примеров после слова «если» стоит условие Т., а после слова «то» — заключение. В такой форме можно высказать каждую Т. Например, Т.: «всякий вписанный в окружность угол, опирающийся на диаметр, прямой», можно высказать так: «если вписанный в окружность угол опирается на диаметр, то он прямой».

Для каждой Т., высказанной в форме «если... то...». можно высказать ей обратную теорему, в которой условие является заключением, а заключение — условием. Прямая и обратная Т. взаимно обратны. Не всякая обратная Т. оказывается верной; так, для примера 1) обратная Т. верна, а для примера 2) — очевидно неверна. Справедливость обеих взаимно обратных Т. означает, что выполнение условия любой из них не только достаточно, но и необходимо для справедливости заключения (см. Необходимые и достаточные условия ) .

Если заменить условие и заключение Т. их отрицаниями, то получится Т., называемая противоположной данной (см. Противоположная теорема ) , она равносильна обратной Т. Точно так же и Т., обратная противоположной, равносильна исходной Т. (прямой). Поэтому доказательство прямой Т. можно заменить доказательством того, что из отрицания заключения данной Т. вытекает отрицание её условия. Этот метод, называемый доказательством от противного, или приведением к абсурду, является одним из наиболее употребительных приёмов математических доказательств.

Теоре'ма СРТ( СРТ -теорема), теорема квантовой теории поля, согласно которой уравнения теории инвариантны относительно СРТ -преобразования, то есть не меняют своего вида, если одновременно провести три преобразования: зарядовое сопряжениеС (замена частиц античастицами ) , пространственную инверсию (зеркальное отражение) Р (замена координат r на — r ) и обращение времени Т (замена времени t на — t ) . Т. СРТ была сформулирована и доказана в работах немецкого физика Г. Людерса (1952— 1954) и швейцарского физика В. Паули (1955). Она вытекает из основных принципов квантовой теории поля. Если в природе происходит некоторый процесс, то в силу Т. СРТ с той же вероятностью в ней может происходить и процесс, в котором частицы заменены соответствующими античастицами, проекции их спинов имеют противоположный знак, а начальные и конечные состояния процесса поменялись местами.

Из Т. СРТ, в частности, следует, что массы и времена жизни частицы и античастицы равны; электрические заряды и магнитные моменты частицы и античастицы отличаются только знаком; взаимодействие частицы и античастицы с гравитационным полем одинаково (нет «антигравитации»); в тех случаях, когда взаимодействие частиц в конечном состоянии пренебрежимо мало, энергетические спектры и угловые распределения продуктов распадов для частиц и античастиц одинаковы, а проекции спинов противоположны.

На опыте ни одного случая нарушения Т. СРТ не обнаружено. Точность, с которой проверено равенство масс частицы и античастицы для 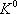- и 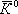-мезонов составляет примерно 10 -15, что на 10 порядков превышает лучшую точность, достигнутую для масс других частиц: ~ 10 -5для электрона (е -) и позитрона (е +), ~ 10 -4для мюонов m -и m +, ~10 -3для К -и К +-мезонов. Равенство времён жизни частиц и античастиц проверено с точностью, не превышающей 10 –3, а равенство магнитных моментов — с точностью ~ 10 -6для m -и m +и ~ 10 -5для е -и е +. Точность сравнения спектров и поляризации в распадах частиц и античастиц, по-видимому, не превышает 10 -2 .

До 1956 существовала уверенность, в том, что законы природы симметричны (одинаковы) относительно каждого из преобразований С , Р и Т в отдельности. Открытие в 1956 нарушений Р- и С-инвариантности, так же, как и открытие в 1964 нарушения СР-инвариантности (см. Комбинированная инверсия ) , почти не затронуло теоретический аппарат физики, который оказался способным включить в себя эти открытия естественным образом, без нарушения фундаментальных принципов теории. В отличие от нарушения Р-, С- и СР-инвариантности, нарушение СРТ -инвариантности, если бы оно было обнаружено на опыте, повлекло бы за собой изменения основ квантовой теории поля. Нарушение Т. СРТ «разорвало» бы связь между частицами и античастицами. В рамках традиционной квантовой теории поля основания Т. СРТ (релятивистская инвариантность, локальность взаимодействия, связь спина и статистики и др.) таковы, что пока не видно, как можно было бы пожертвовать хотя бы одним из них, не изменив радикально всю теорию. В не меньшей степени это справедливо и в отношении аксиоматической квантовой теории поля. Тем интереснее представляются экспериментальные поиски эффектов проявления СРТ -неинвариантности.

Лит.: Лапидус Л. И., Следствия СРТ-инварнантностп и эксперимент, «Успехи физических наук», 1968, т. 95, в. 4; Файнберг В. Я., Теоретические основы СРГ-инвариантности, там же, в. 3.

Л. Б. Окунь.

«Теорети'ческая и математи'ческая фи'зика»,научный журнал Секции физико-технических и математических наук Президиума АН СССР. Публикует оригинальные статьи физического и математического содержания по фундаментальным проблемам строения материи. Издаётся в Москве с 1969. Ежегодно выходит 4 тома, каждый из которых состоит из 3 выпусков. Тираж (1976) около 1100 экземпляров.

Теорети'ческой астроно'мии институ'т(ИТА), научно-исследовательское учреждение АН СССР в Ленинграде, ведущее работы в области всех теоретических и прикладных проблем небесной механики. Одна из основных задач ИТА — издание «Астрономического ежегодника СССР» и других справочных изданий по астрономии. ИТА начал деятельность в 1919 как Вычислительный институт при Всероссийском астрономическом союзе. В 1923 объединён с Астрономо-геодезическим институтом (основан в 1920) и переименован в Астрономический институт. Тематика института была расширена (небесная механика, гравиметрия, астрофизика, приборостроение). С 1943 на институт была возложена научно-исследовательская работа в области небесной механики и эфемеридной астрономии, в связи с чем он получил современное название. С 1948 ИТА, по предложению Международного астрономического союза, стал международным центром по изучению малых планет. С 1957 ИТА разрабатывает также проблемы движения искусственных небесных тел ( астродинамика ) . институт издаёт Бюллетень (с 1924) и Труды (с 1952).