БСЭ БСЭ - Большая Советская Энциклопедия (ФА)

Примеры Ф. п. II рода – появление (ниже определённой в каждом случае температуры) магнитного момента у магнетика при переходе парамагнетик – ферромагнетик, антиферромагнитного упорядочения при переходе парамагнетик – антиферромагнетик, возникновение сверхпроводимости в металлах и сплавах, возникновение сверхтекучести в 3He и 4He, упорядочение сплавов, появление самопроизвольной (спонтанной) поляризации вещества при переходе параэлектрик – сегнетоэлектрик и т.д.

Л. Д. Ландау (1937) предложил общую трактовку всех Ф. п. II рода, как точек изменения симметрии: выше точки перехода система обладает более высокой симметрией, чем ниже точки перехода. Например, в магнетике выше точки перехода направления элементарных магнитных моментов ( спинов ) частиц распределены хаотически. Поэтому одновременный поворот всех спинов не меняет физических свойств системы. Ниже точки перехода спины имеют преимущественную ориентацию. Одновременный их поворот изменяет направление магнитного момента системы. Другой пример: в двухкомпонентном сплаве, атомы которого А и В расположены в узлах простой кубической кристаллической решётки, неупорядоченное состояние характеризуется хаотическим распределением атомов А и В по узлам решётки, так что сдвиг решётки на один период не меняет её свойств. Ниже точки перехода атомы сплава располагаются упорядоченно: ... ABAB... Сдвиг такой решётки на период приводит к замене всех атомов А на В или наоборот. В результате установления порядка в расположении атомов симметрия решётки уменьшается.

Сама симметрия появляется и исчезает скачком. Однако величина, характеризующая асимметрию (параметр порядка), может изменяться непрерывно. При Ф. п. II рода параметр порядка равен нулю выше точки перехода и в самой точке перехода. Подобным образом ведёт себя, например, магнитный момент ферромагнетика, электрическая поляризация сегнетоэлектрика, плотность сверхтекучей компоненты в жидком 4He, вероятность обнаружения атома А в соответствующем узле кристаллической решётки двухкомпонентного сплава и т.д.

Для Ф. п. II рода характерно отсутствие скачков плотности, концентрации, теплоты перехода. Но точно такая же картина наблюдается и в критической точке на кривой Ф. п. I рода (см. Критические явления ) . Сходство оказывается очень глубоким. Вблизи критической точки состояние вещества можно характеризовать величиной, играющей роль параметра порядка. Например, в случае критической точки на кривой равновесия жидкость – пар это – отклонение плотности от среднего значения. При движении по критической изохоре со стороны высоких температур газ однороден, и эта величина равна нулю. Ниже критической температуры, вещество расслаивается на две фазы, в каждой из которых отклонение плотности от критической не равно нулю. Поскольку вблизи точки Ф. п. II рода фазы мало отличаются друг от друга, возможно образование зародышей большого размера одной фазы в другой ( флуктуации ) , точно так же, как вблизи критической точки. С этим связаны многие критические явления при Ф. п. II рода: бесконечный рост магнитной восприимчивости ферромагнетиков и диэлектрической постоянной сегнетоэлектриков (аналогом является рост сжимаемости вблизи критической точки жидкость – пар), бесконечный рост теплоёмкости, аномальное рассеяние электромагнитных волн [световых в жидкости и паре (см. Опалесценция критическая ) , рентгеновских в твёрдых телах], нейтронов в ферромагнетиках. Существенно меняются и динамические явления, что связано с очень медленным рассасыванием образовавшихся флуктуаций. Например, вблизи критической точки жидкость – пар сужается линия рэлеевского рассеяния света, вблизи Кюри точки ферромагнетиков и Нееля точки антиферромагнетиков замедляется спиновая диффузия (см. Спиновые волны ) и т.д. Средний размер флуктуаций (радиус корреляции) R растет по мере приближения к точке Ф. п. II рода и становится в этой точке бесконечно большим.

Современные достижения теории Ф. п. II рода и критических явлений основаны на гипотезе подобия. Предполагается, что если принять R за единицу измерения длины, а среднюю величину параметра порядка ячейки с ребром R – за единицу измерения параметра порядка, то вся картина флуктуаций не будет зависеть ни от близости к точке перехода, ни от конкретного вещества. Все термодинамические величины являются степенными функциями R. Показатели степеней называют критическими размерностями (индексами). Они не зависят от конкретного вещества и определяются лишь характером параметра порядка. Например, размерности в точке Кюри изотропного материала, параметром порядка которого является вектор намагниченности, отличаются от размерностей в критической точке жидкость – пар или в точке Кюри одноосного магнетика, где параметр порядка – скалярная величина.

Вблизи точки перехода уравнение состояния имеет характерный вид закона соответственных состояний. Например, вблизи критической точки жидкость – пар отношение 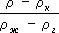зависит только от 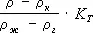(здесь r- плотность, r к - критическая плотность, r ж – плотность жидкости, r г – плотность газа, p – давление, p k– критическое давление, К т– изотермическая сжимаемость ) , причём вид зависимости при подходящем выборе масштаба один и тот же для всех жидкостей (см. Критические явления ) .

Достигнуты большие успехи в теоретическом вычислении критических размерностей и уравнений состояния в хорошем согласии с экспериментальными данными. Приближенные значения критических размерностей приведены в таблице.

Таблица критических размерностей термодинамических и кинетических величин

* Изменение плотности с давлением, намагниченности с напряжённостью магнитного поля и др. T k– критическая температура.

Дальнейшее развитие теории Ф. п. II рода связано с применением методов квантовой теории поля, в особенности метода ренормализационной группы. Этот метод позволяет, в принципе, найти критические индексы с любой требуемой точностью.

Деление Ф. п. на два рода несколько условно, т.к. бывают Ф. п. I рода с малыми скачками теплоёмкости и др. величин и малыми теплотами перехода при сильно развитых флуктуациях. Ф. п. – коллективное явление, происходящее при строго определённых значениях температуры и др. величин только в системе, имеющей в пределе сколь угодно большое число частиц.