БСЭ БСЭ - Большая Советская Энциклопедия (ФЕ)

Соч.: Пианизм как искусство, 2 изд.. М., 1969.

Лит.: Алексеев Л., О пианистических принципах С. Е. Фейнберга, в кн.: Мастера советской пианистической школы. Очерки, М., 1954.

В. А. Натансон.

Фе'йнман(Feynman) Ричард Филлипс (р. 11.5.1918, Нью-Йорк), американский физик. Окончил Массачусетсский технологический институт (1939), получил степень доктора философии в Принстонском университете (1942): затем работал в Лос-Аламосской лаборатории и Корнеллском университете. С 1950 профессор Калифорнийского технологического института (Пасадена). Основные труды по квантовой электродинамике, квантовой механике и статистической физике. Разработал математический аппарат (см. Фейнмана диаграммы ) , сыгравший важную роль в развитии квантовой теории поля (Нобелевская премия, 1965). В статистической физике предложил теорию полярона для случая промежуточной связи, объяснил появление вихрей в сверхтекучем гелии (вихри Фейнмана). Разработал метод интегрирования по траекториям в квантовой механике. Автор курса лекций для вузов, в котором существенно модернизировано традиционное изложение физики (в рус. пер. – «Фейнмановские лекции по физике», в. 1–9, М., 1965–67; совместно с Р. Лейтоном и М. Сэндсом).

Соч. в рус. пер.: Теория позитронов, в сборнике: Новейшее развитие квантовой электродинамики, М., 1954; Пространственно-временная трактовка квантовой электродинамики, там же, с. 161 – 204; Квантовая электродинамика, М., 1964; Квантовая механика и интегралы по траекториям, М., 1968 (совм. с А. Хибсом): Статистическая механика, М., 1975.

Д. Н. Зубарев.

Фе'йнмана диагра'ммы,Фейнмана графики, графический метод теоретического анализа рассеяния частиц и др. физических процессов и вычисления их амплитуд. Предложен Р. Фейнманом в 1949, сыграл важнейшую роль в развитии квантовой электродинамики. Ф. д. нашли широкое применение в квантовой теории поля, квантовой механике и статистической физике.

Основное понятие в методе Ф. д. – функция распространения, или пропагатор. Движению частицы в квантовой теории ставится в соответствие процесс распространения волнового поля, поле же в каждой точке пространства в каждый момент времени является источником вторичных волн (принцип Гюйгенса). Пропагатор характеризует распространение такой волны между двумя пространственно-временными точками. Он является функцией этих двух точек ( 1 и 2 ) и изображается линией, их соединяющей ( рис. 1 ). Поле в точке 2 определяется суммой волн, испущенных из всевозможных точек 1 .

Взаимодействие в квантовой теории рассматривается как испускание и поглощение волн (частиц) различного типа. Например, электромагнитное взаимодействие сводится к испусканию или поглощению электронной волной (электроном) электромагнитной волны (фотона). Элементарный акт такого взаимодействия изображается графически диаграммой рис. 2 , в которой прямые линии – пропагаторы электрона, волнистая – фотона. Эта диаграмма означает, что при распространении электронной волны из 1 в 2 в точке 3 появилось электромагнитное поле, испущенное в точке 4 – точке перессчения линий, называемой вершиной диаграммы. С помощью диаграммы рис. 2 как основного элемента можно построить Ф. д. для любого электродинамического процесса. Например, диаграммы рис. 3 и 4 изображают соответственно рассеяние (столкновение) электрона и фотона на электроне. Внешние линии изображают частицы (электрон или фотон) до и после столкновения, а внутренние элементы (вершины и линии) – механизм взаимодействия, который сводится на рис. 3 к излучению электромагнитной волны одним электроном и поглощению её вторым, а на рис. 4 электронной волны. Т. о., распространению волны между двумя вершинами (т. е. внутренние линии) отвечает движение соответствующей частицы в виртуальном состоянии (см. Виртуальные частицы ) . Одна и та же внешняя линия может изображать как начальную частицу, так и конечную античастицу (и наоборот). Например, диаграмма рис. 4 может изображать (следует смотреть на неё не слева направо, а снизу вверх) аннигиляцию пары электрон-позитрон в два фотона.

Приведённые Ф. д. отвечают минимальному числу элементарных взаимодействий, т. е. вершин в диаграмме, приводящих к данному процессу. Но они не единственно возможные. Данный тип столкновения частиц определяется внешними линиями (начальными и конечными частицами), внутренняя же часть диаграммы может быть более сложной. Например, для рассеяния фотона электроном можно привести в дополнение к диаграмме рис. 4 Ф. д., изображенные на рис. 5 , и многие другие.

На диаграммах рис. 5 электрон (падающий или виртуальный) испускает виртуальный фотон, который поглощается конечным электроном (на последней диаграмме этот фотон рождает виртуальную пару электрон-позитрон, аннигилирующую в фотон). Если взаимодействие мало, то Ф. д. рис. 5 и другие, содержащие большее число вершин, т. е. большее число элементарных взаимодействий, дадут лишь малые поправки (они называются радиационными поправками ) по сравнению с вкладом основной диаграммы рис. 4 , и можно ограничиться небольшим числом диаграмм. Это справедливо для квантовой электродинамики, в которой каждая дополнительная внутренняя линия вносит в амплитуду рассеяния рассматриваемого процесса множитель 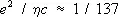где е – заряд электрона, 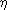– постоянная Планка, с – скорость света; поэтому квантовая электродинамика достигла высокой точности предсказаний. Если же взаимодействие не мало, то следует учитывать бесконечное число диаграмм, и это – трудность квантовой теории поля.

Ф. д. используются также для изображения процессов, обусловленных др. типами взаимодействий. На рис. 6 приведен распад p 0-мезона; здесь пунктирная линия – p 0, сплошные линии – нуклон и антинуклон (или кварк и антикварк), левая вершина – сильное взаимодействие, волнистые линии – фотоны, а соответствующие (правые) вершины – электромагнитные взаимодействия. На рис. 7 приведён распад заряженного p-мезона; пунктирная линия – p +(p -), линии в петле – нуклон и антинуклон (кварк и антикварк), волнистая линия – гипотетический W +(W -)-meзон, переносчик слабого взаимодействия, сплошные линии справа – мюон и нейтрино.