БСЭ БСЭ - Большая Советская Энциклопедия (ЦИ)

Лит.: Строева О. Г., Морфогенез и врожденные аномалии глаза млекопитающих, М., 1971; Davson Н., The physiology of the eye, 3 ed., Edin. — L., 1972.

О. Г. Строева.

Цили'ндр(от греч. kýlindros — валик, каток), тело, ограниченное замкнутой цилиндрической поверхностью и двумя секущими её параллельными плоскостями — основаниями Ц. ( рис. ). Если основания перпендикулярны образующей, то Ц. называется прямым; в частности, если основания представляют собой круги, то говорят о прямом круговом, или круглом, Ц., который часто называется просто цилиндром. Объём такого Ц. равен V = p r 2h, боковая поверхность S = 2p rh (где r — радиус основания, h — высота).

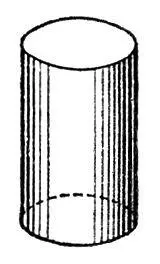
К ст. Цилиндр.

Цили'ндр,деталь машины, имеющая внутреннюю цилиндрическую полость, в которой может перемещаться поршень или плунжер, изменяя объём полостей по одну и др. сторону поршня. В Ц. преобразуется энергия подаваемого в него рабочего тела (пара, горючей смеси), оказывающего давление на поршень, в энергию движения поршня (в тепловых двигателях) или энергия движения поршня — в энергию жидкости или газа (в насосах или компрессорах). Если используется полость с одной стороны поршня, то Ц. закрывают крышкой с одного конца, если же используют обе полости, то предусматривают две крышки и шток, связывающий поршень с ползуном. В гидравлическом и пневматическом приводах поступательные движения (в металлорежущих станках, прессах, подъёмниках), а также в некоторых поршневых машинах Ц. выполняют в виде обособленной детали. В многоцилиндровых поршневых машинах (в двигателях внутреннего сгорания и др.) Ц. часто объединяют в общий блок, располагая их в ряд (рядный двигатель), под углом (V-образный двигатель) или друг против друга (оппозитный двигатель), — т. н. блок Ц. В насосах и гидромоторах бесступенчатых приводов вращательного движения Ц. часто размещают в роторе радиально или параллельно оси ротора.

Н. Я. Ниберг.

Цилиндри'ческая пове'рхность,поверхность, описываемая прямой линией (образующей Ц. п.), которая движется, оставаясь параллельной заданному направлению и скользя по заданной кривой (направляюще и). Если ось Oz прямоугольной системы координат параллельна образующей Ц. п., то уравнение Ц. п. будет F ( x, у ) = 0 . Если образующие Ц. п. параллельны прямой ax + by + с = 0, лежащей в плоскости хОу, то уравнение Ц. п. имеет вид z = f ( ax + by ) . Если направляющей служит окружность, эллипс, гипербола или парабола, то Ц. п. называется соответственно круглым, эллиптическим, гиперболическим или параболическим цилиндром.

Цилиндри'ческая прое'кция,один из видов картографических проекции.

Цилиндри'ческие зме'и(Cylindrophis), род пресмыкающихся семейства вальковатых змей. Длина до 78 см. Окраска яркая. 5 видов. Распространены в Юго-Восточной Азии и на островах, прилежащих к Австралии. Наиболее известна красная Ц. з. (С. rufus); ведёт роющий образ жизни, питается слепозмейками и др. мелкими змеями, а также дождевыми червями и личинками насекомых. В случае опасности приподнимает кверху короткий толстый хвост, отвлекая внимание врага от плотно прижатой к земле головы. Живородящи.

Цилиндри'ческие координа'тыточки М, три числа r , q, z, характеризующие положение точки в пространстве (см. рис. ). Наименование Ц. к. связано с тем, что координатная поверхность (см. Координаты ) r = const является цилиндром, образующие которого параллельны Oz. Ц. к. и прямоугольные координаты х, у, z точки М связаны соотношениями: х = r cosq, у = r sinq, z = z.

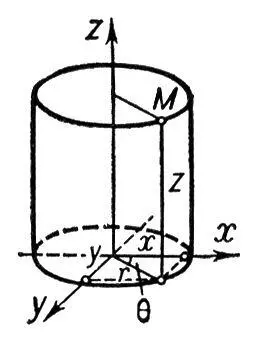
К ст. Цилиндрические координаты.

Цилиндри'ческие магни'тные доме'ны,«магнитные пузырьки», изолированные однородно намагниченные подвижные области ферро- или ферримагнетика ( домены ) , имеющие форму круговых цилиндров и направление намагниченности, противоположное направлению намагниченности остальной его части ( рис. 1 ). Обнаружены в конце 50-х гг. 20 в. в ортоферритах и гексаферритах, предложение о практическом использовании Ц. м. д. в вычислительной технике относится к 1967. На практике Ц. м. д. получают в тонких (1—100 мкм ) плоскопараллельных пластинах (плёнках) монокристаллических ферримагнетиков (ферриты-гранаты) или аморфных ферромагнетиков (сплавы d- и f- переходных элементов с единственной осью лёгкого намагничивания, направленной перпендикулярно поверхности пластины). Магнитное поле, формирующее Ц. м. д. (поле подмагничивания), прикладывается по оси лёгкого намагничивания. В отсутствии внешнего подмагничивающего поля доменная структура пластин имеет неупорядоченный лабиринтообразный вид ( рис. 2 , а) . При наложении подмагничивающего поля домены, не имеющие контакта с краями пластины, стягиваются и образуют Ц. м. д. ( рис. 2 , б) . Вектор намагниченности Ц. м. д. J ориентируется вдоль оси лёгкого намагничивания.

Изолированные Ц. м. д. существуют в определённом интервале полей подмагничивания, который составляет несколько процентов от величины намагниченности насыщения материала. Нижняя граница интервала устойчивости соответствует переходу Ц. м. д. в домены иной формы, верхняя — исчезновению (коллапсу) Ц. м. д. Устойчивое существование Ц. м. д. обусловлено равновесием трёх сил: силы взаимодействия намагниченности Ц. м. д. с полем подмагничивания; силы, связанной с существованием у Ц. м. д. стенок (аналогична силе поверхностного натяжения); наконец, силы взаимодействия намагниченности Ц. м. д. с размагничивающим полем остальной части магнетика. Первые две силы стремятся сжать Ц. м. д., а третья — растянуть. В момент формирования радиус Ц. м. д. имеет максимальную величину; при дальнейшем увеличении подмагничивающего поля радиус Ц. м. д. уменьшается, а при некотором поле Н к сжимающие силы начинают превышать растягивающие и Ц. м. д. исчезают (коллапсируют) ( рис. 3 ). Реальные размеры Ц. м. д. зависят, помимо поля подмагничивания, от физических параметров материала и толщины плёнки. В центре интервала устойчивости диаметр Ц. м. д. примерно равен толщине плёнки.