БСЭ БСЭ - Большая Советская Энциклопедия (ЧЕ)

С понятием Ч. тесно связан фундаментальный вопрос о симметрии реального пространства относительно зеркальных отражений. Методами теории групп доказывается, что если пространство обладает зеркальной симметрией, то должны строго выполняться либо закон сохранения Ч., либо инвариантность при комбинированной инверсии. Экспериментально установлено нарушение обоих этих законов при слабых взаимодействиях. Поэтому есть основание считать, что либо пространство не обладает симметрией между правым и левым, либо эта симметрия нарушается в определённых типах взаимодействий (например, приводящих к распаду т. н. долгоживущего нейтрального К-мезона, 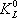® 2p).

Лит.: Ли Ц., Ву Ц., Слабые взаимодействия, пер. с англ., М., 1968; Широков Ю. М., Юдин Н. П., Ядерная физика, М., 1972; Ли Цзун-дао, Янг Чжэнь-нин, в сборнике: Новые свойства симметрии элементарных частиц, пер. с англ., М., 1957, с. 13; Ву Цзянь-сюн [и др.], там же, с. 69; Гарвин Р., Ледерман Л., Вейнрих М., там же, с. 75; Abov Yu. G. et al, «Physics Letters», 1968, v. 27B, № 1, p. 16; Лобашов В. М., «Вестник АН СССР», 1969, № 2, с, 58; Вигнер Е., «Успехи физических наук», 1958, т. 65, в. 2, с. 257; Wick G., Wightman A., Wigner Е., «Physical Review», 1952, v. 88, p. 101; Ландау Л. Д., «Журнал экспериментальной и теоретической физики», 1957, т. 32, в. 2, с. 405; Широков Ю. М., там же, 1958, т. 34, в. 3, с. 717; его же, там же, 1960, т. 38, в. 1, с. 140.

Ю. М. Широков.

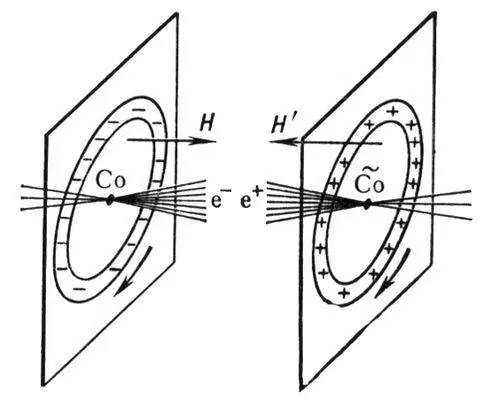
К ст.Чётность.

Чётность у'ровня, чётность состояния физической системы (чётность волновой функции), соответствующего данному уровню энергии. Такая характеристика уровней энергии возможна для системы частиц, между которыми действуют электромагнитные или ядерные силы, сохраняющие чётность. При учёте слабых взаимодействий к состоянию с данной чётностью добавляется незначительную примесь состояния с противоположной чётностью (в атомных ядрах относительная величина такой примеси порядка 10 ¾6¾ 10 —7). Если уровень энергии вырожден так, что ему принадлежат волновые функции с разной чётностью (как это, например, имеет место для возбуждённых уровней атома водорода), то возможны состояния, описываемые суперпозицией таких волновых функций, т. е. уровень может не обладать определённой чётностью (даже если действующие в системе силы сохраняют чётность).

С. С. Герштейн.

Чётные и нечётные фу'нкции(матем.). Функция у = f ( x ) называется чётной, если она не меняется, когда независимое переменное изменяет только знак, то есть, если f ( —x ) = f ( x ) . Если же f ( —x ) = — f ( x ), то функция f ( x ) называется нечётной. Например, у = cos x , у = x 2 — чётные функции, а = у sin x , у = x 3— нечётные. График чётной функции симметричен относительно оси Оу , график нечётной функции симметричен относительно начала координат.

«Четы'ре иску'сства»,Общество художников «4 искусства», художественное объединение, существовавшее в Москве в 1924—31. Основано главным образом бывшими членами «Мира искусства» и «Голубой розы». Включало советских живописцев, графиков, скульпторов и архитекторов преимущественно старшего поколения (Л. А. Бруни, И. С. Ефимов, И. В. Жолтовский, К. Н. Истомин, А. И. Кравченко, П. В. Кузнецов, Н. Н. Купреянов, А. Т. Матвеев, В. И. Мухина, А. П. Остроумова-Лебедева, К. С. Петров-Водкин, М. С. Сарьян, В. А. Фаворский, А. В. Щусев и др.). Для членов объединения характерны стремление к высокому профессиональному мастерству, широким образным обобщениям и выразительной декоративности в изобразительных искусствах, разработка принципов современного градостроительства. «Ч. и.» организовывало выставки в Москве (1925, 1926, 1929) и в Ленинграде (1928).

Лит.: Бебутова Е., Кузнецов П., Общество «4 искусства», «Творчество», 1966, № 11.

«Четы'ре пра'жских статьи'»,см. Пражские статьи 1420.

«Четы'ре семе'йства» Кита'я,реакционная гоминьдановская группировка, правившая Китаем с 1927 по 1949. Состояла из представителей семейств Чан Кай-ши , Сун Цзы-вэня, Кун Сян-си и братьев Чэнь Го-фу и Чэнь Ли-фу, возглавлял её Чан Кай-ши. Захватив государственную власть и монополизировав основные командные высоты в экономике страны, «Ч. с.» К. подвергали китайский народ жестокой эксплуатации. За 22 года господства в Китае они сконцентрировали в своих руках капитал, превышающий 20 млрд. американских долл. Господство в стране «Ч. с.» К. опиралось на поддержку империалистических держав, особенно США. Позиции США в гоминьдановском Китае заметно усилились. После победы народной революции (1949) капитал «Ч. с.» К. был конфискован и превращен в государственную собственность КНР.

Лит.: Чэнь Бода, Четыре семейства Китая, пер. с кит., М., 1948.

Четырёх кра'сок зада'ча,задача, заключающаяся в доказательстве (или опровержении) следующего предложения: четырёх различных красок достаточно для того, чтобы раскрасить любую карту так, чтобы никакие две области, имеющие общий участок границы, не были окрашены в один и тот же цвет. Это предложение подтверждается во всех известных частных случаях (сообщение о его доказательстве было опубликовано лишь в 1976).

В качестве математической задачи оно было сформулировано впервые в середине 19 в. и получило широкую известность благодаря лекциям английского математика О. де Моргана. Чтобы поставить задачу с полной строгостью, надо потребовать, чтобы рассматриваемые области были ограничены простыми замкнутыми контурами (замкнутыми жордановыми кривыми). Без труда можно доказать, что пяти красок всегда достаточно для раскраски такого рода «карты». Если же соответствующую задачу формулировать для пространства, то здесь никакое число «красок» не окажется достаточным.

Лит.: Appel К., Haken W., «Bulletin of the American Mathematical Society», 1976, v. 82, № 5, p. 711—12.

Четырёхгла'зки(Anableps), род живородящих рыб семейства четырёхглазковых отряда карпозубообразных. Длина тела 15—20 см , редко до 30 см. Глаз у Ч. (роговица и сетчатка) разделён эпителиальной перегородкой на 2 части — верхнюю и нижнюю. Верхние половины глаз приспособлены для зрения вне воды. Это позволяет Ч., плавающей обычно у поверхности воды, видеть одновременно над и под водой. Известно 2 вида. Ч. обитают в лагунах Центральной Америки и северной части Южной Америки. Питаются мелкими беспозвоночными (главным образом воздушными насекомыми), выслеживая их в воде и над её поверхностью. Оплодотворение у Ч. внутреннее. Вымётывают 1—5 мальков длиной 4—6 см.