БСЭ БСЭ - Большая Советская Энциклопедия (ЭЛ)
- Название:Большая Советская Энциклопедия (ЭЛ)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (ЭЛ) краткое содержание
Большая Советская Энциклопедия (ЭЛ) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
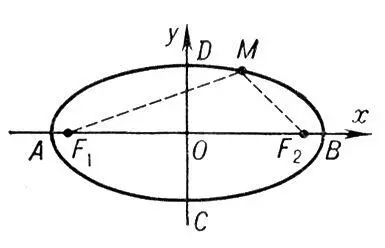
Рис. 2. к ст. Эллипс.

Рис. 1. к ст. Эллипс.
Эллипс инерции
Э'ллипс ине'рциив сопротивлении материалов, графическое изображение, используемое для вычисления осевых и центробежных моментов инерции плоской фигуры (например, поперечного сечения стержня) относительно осей, проходящих через её центр тяжести. При построении Э. и. его полуоси, численно равные главным радиусам инерции фигуры, совмещаются с её главными центральными осями.
Эллипс (пропуск в речи)
Э'ллипс(от греч. elleipsis — нехватка, опущение, выпадение), пропуск в речи (тексте) подразумеваемой языковой единицы: звука или звукосочетания (обычно в разговорной речи: «када» — когда, «мож-быть» — может быть), слова (словосочетания), названного в контексте («У отца был большой письменный стол, а у сына маленький»), составляющего часть фразеологического оборота («Ты в любом случае выйдешь сухим» [из воды]), предсказываемого значением и (или) формой др. слов («Ты на работу?» [идёшь]; [Я] «сижу за решёткой в темнице сырой...» — Пушкин), ясного из ситуации («Мне чёрный» [кофе, хлеб...]). Э. синтаксического члена, не восстанавливаемого однозначно, носит экспрессивный, эмоциональный характер и используется как фигура стилистическая («Я за свечку, свечка — в печку», К. Чуковский).
Эллипсоид
Эллипсо'ид(от эллипс и греч. eidos — вид), замкнутая центральная поверхность второго порядка. Э. имеет центр симметрии О (см. рис. ) и три оси симметрии, которые называются осями Э. Точки пересечения координатных осей с Э. называются его вершинами. Сечения Э. плоскостями являются эллипсами (в частности, всегда можно указать круговые сечения Э.). В надлежащей системе координат уравнение Э. имеет вид:
x 2/ a 2+ y 2/ b 2+ z 2/ c 2= 1.
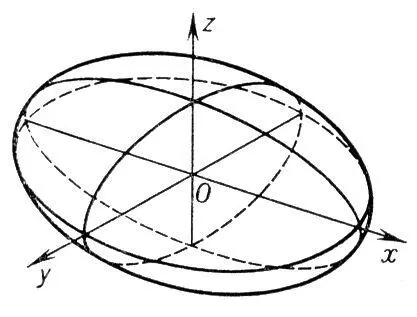
Рис. к ст. Элипсоид.
Эллиптическая геометрия
Эллипти'ческая геоме'трия,то же, что Римана геометрия.
Эллиптическая точка
Эллипти'ческая то'чкаповерхности, точка, в которой полная кривизна поверхности положительна. В окрестности Э. т. поверхность расположена по одну сторону от своей касательной плоскости.
Эллиптические галактики
Эллипти'ческие гала'ктики,гигантские звёздные системы, имеющие форму эллипсоида. Э. г., как правило, не содержат космической пыли. См. Галактики.
Эллиптические интегралы
Эллипти'ческие интегра'лы,интегралы вида
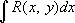 ,
,
где R ( x, у ) — рациональная функция х и 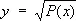 , а Р ( х ) — многочлен 3-й или 4-й степени без кратных корней.
, а Р ( х ) — многочлен 3-й или 4-й степени без кратных корней.
Под Э. и. первого рода понимают интеграл
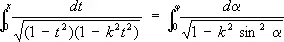 (1)
(1)
под Э. и. второго рода — интеграл
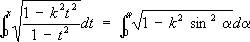
где k — модуль Э. и., 0 < k < 1 ( х = sin j, t = sin a. Интегралы в левых частях равенств (1) и (2) называются Э. и. в нормальной форме Якоби, интегралы в правых частях — Э. и. в нормальной форме Лежандра. При х = 1 или j = p/2 Э. и называются полными и обозначаются, соответственно, через
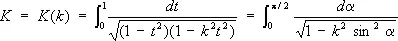
и
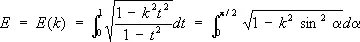
Своё назв. Э. и. получили в связи с задачей вычисления длины дуги эллипса и = a sin a , v = b cos a( a < b ) . Длина дуги эллипса выражается формулой
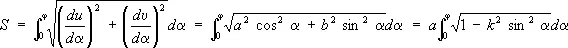
где 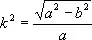 — эксцентриситет эллипса. Длина дуги четверти эллипса равна E ( k ) . Функции, обратные Э. и., называются эллиптическими функциями.
— эксцентриситет эллипса. Длина дуги четверти эллипса равна E ( k ) . Функции, обратные Э. и., называются эллиптическими функциями.
Эллиптические координаты
Эллипти'ческие координа'ты,координаты, связанные с семейством софокусных эллипсов и гипербол (см. Софокусные кривые ) . Э. к. точки М и её декартовы координаты х, у связаны соотношениями х = с ch u cos v, у = с sh u sin v.
Эллиптические траектории
Эллипти'ческие траекто'рии, траектории, которые может описывать материальная точка (или центр масс тела) при движении под действием силы ньютонианского тяготения. В поле тяготения Земли, если пренебречь сопротивлением среды, Э. т. будет в 1-м приближении траектория центра масс тела, которому вблизи поверхности Земли сообщена начальная скорость 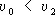 , где
, где 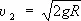 » 11,2 км/сек — вторая космическая скорость ( R — радиус Земли, g — ускорение силы тяжести).
» 11,2 км/сек — вторая космическая скорость ( R — радиус Земли, g — ускорение силы тяжести).
Эллиптические функции
Эллипти'ческие фу'нкции,функции, связанные с обращением эллиптических интегралов. Э. ф. применяются во многих разделах математики и механики как при теоретических исследованиях, так и для численных расчётов.
Подобно тому как тригонометрическая функция u = sinx является обратной по отношению к интегралу
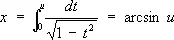
так обращение нормальных эллиптических интегралов 1-го рода
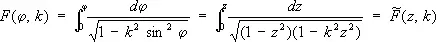
где z = sin jw, k — модуль эллиптического интеграла, порождает функции: j = am z — амплитуда z (эта функция не является Э. ф.) и w = sn z = sin (am z ) — синус амплитуды. Функции cn — косинус амплитуды и dn z — дельта амплитуды определяются формулами
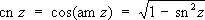
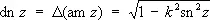
Интервал:
Закладка:
