БСЭ БСЭ - Большая Советская Энциклопедия (ЭЛ)
- Название:Большая Советская Энциклопедия (ЭЛ)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (ЭЛ) краткое содержание
Большая Советская Энциклопедия (ЭЛ) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Функции sn z, cn z, dn z называют Э. ф. Якоби. Они связаны соотношением
sn 2 z + cn 2z = k 2sn 2 z + dn 2 z = 1.
На рис. представлен вид графиков Э. ф. Якоби. Они связаны соотношением
sn 2 z + cn 2z = k 2sn 2 z + dn 2 z = 1
На рис. представлен вид графиков Э. ф. Якоби для действительного x и 0 < k < 1; а
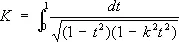
— полный нормальный эллиптический интеграл 1-го рода и 4 K — основной период Э. ф. sn z. В отличие от однопериодической функции sin х, функция sn z — двоякопериодическая. Её второй основной период равен 2 iK, где
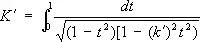
и 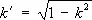 — дополнительный модуль. Периоды, нули и полюсы Э . ф. Якоби приведены в таблице, где m и n — любые целые числа.
— дополнительный модуль. Периоды, нули и полюсы Э . ф. Якоби приведены в таблице, где m и n — любые целые числа.
| Функции | Периоды | Нули | Полюсы |
| sn z | 4 Km + 2 iK'n | 2 mK + 2 iK'n | }2 mK + (2 n + 1) iK' |
| cn z | 4 K + (2 K + 2 iK' ) n | (2 m + 1) K + 2 iK'n | |
| dn z | 2 Km + 4 iK'n | (2 m + 1) K + (2 n + 1) iK |
Э. ф. Вейерштрасса Ã( х ) может быть определена как обратная нормальному эллиптическому интегралу Вейерштрасса 1-го рода
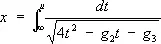
где параметры g 2и g 2— называются инвариантами Ã( x ) . При этом предполагается, что нули e 1, e 2и e 3многочлена 4 t 3— g 2 t — g 3 различны между собой (в противном случае интеграл (*) выражался бы через элементарные функции). Э. ф. Вейерштрасса Ã( х ) связана с Э. ф. Якоби следующими соотношениями:
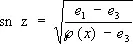 ,
,
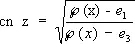 ,
,
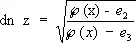 .
.
Любая мероморфная двоякопериодическая функция f ( z ) с периодами w 1и w 2, отношение которых мнимо, т. е. f ( z + m w 1+ п w 2) = f ( z ) при m , n = 0 , ± 1, ±2,... и 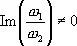 , является Э. ф. Для построения Э. ф., а также численных расчётов применяют сигма-функции и тэта-функции.
, является Э. ф. Для построения Э. ф., а также численных расчётов применяют сигма-функции и тэта-функции.
Изучению Э. ф. предшествовало накопление знаний об эллиптических интегралах, систематическое изложение теории которых дал А. Лежандр. Основоположниками теории Э. ф. являются Н. Абель (1827) и К. Якоби (1829). Последний дал развёрнутое изложение теории Э. ф., названное его именем. В 1847 Ж. Лиувилль опубликовал изложение основ общей теории Э. ф., рассматриваемых как мероморфные двоякопериодические функции. Представление Э. ф. через Ã-функцию, а также z-, s-функции дано К. Вейерштрассом в 40-х гг. 19 в. (две последние не являются Э. ф.).
Лит.: Маркушевич А. И., Теория аналитических функций, 2 изд., т. 2, М., 1968; Гурвиц А., Курант Р., Теория функций, пер. с нем., М., 1968; Уиттекер Э, Т., Ватсон Дж. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963; Бейтмен Г., Эрдейи А., Высшие трансцендентные функции. Эллиптические и автоморфные функции. Функции Ламе и Матье, пер. с англ., М., 1967.
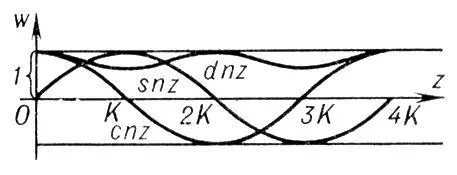
Рис. к ст. Эллиптические функции.
Эллиптический параболоид
Эллипти'ческий параболо'ид,один из двух видов параболоидов.
Эллиптический цилиндр
Эллипти'ческий цили'ндр,линейчатая цилиндрическая поверхность, уравнение которой может быть приведено к виду x 2/ a 2 + y 2 b 2= 1. См. Поверхности второго порядка.
Эллис (атоллы)
Э'ллис(Ellice) (с 1975 — Тувалу; Tuvalu), группа атоллов на З. Тихого океана, в Полинезии. Владение Великобритании. Площадь 24 км 2 . Население 5,8 тыс. человек (1973). Состоит из 9 низменных коралловых атоллов, вытянутых на 600 км. Плантации кокосовой пальмы, бананов. Экспорт копры. Административный центр — г. Фунафути.
Эллис Фред
Э'ллис(Ellis) Фред (5.6. 1886, Чикаго, — 10. 6. 1965, Нью-Йорк), американский график-карикатурист. С 1924 член компартии США. Учился в художественной школе в Чикаго (1905), с 1927 главный художник «Дейли уоркер», в 1930—36 работал в СССР для газет «Правда» и «Труд». В ясных, широких и живописных по манере рисунках Э. нашли страстное и лаконичное выражение темы обличения капитализма, призыв к борьбе рабочего класса, гневное осуждение фашизма.
Лит.: Дурус А., Фред Эллис, М. — Л., 1937; Выгодская Т., Фред Эллис, «Искусство», 1964, № 11.

Ф. Эллис. «Не беспокойтесь, здесь только коммунисты». Рисунок. 1934.
Эллора
Элло'ра,Эллур, Элура, деревня в Индии, в 15 км от Аурангабада (штат Махараштра), близ которой — группа из 34 высеченных в скале буддийских, брахманских и джайнских храмов (все — между 6—13 вв.), в том числе монолитный храм Кайласанатха, стилобат одной из трёх частей которого опоясан изваяниями слонов в натуральную величину.
Элляй
Элля'й(литературное имя; настоящее имя и фамилия Серафим Романович Кулачиков) [16(29). 11. 1904, Нижнеамгинский наслег Ботурусского улуса, ныне Алексеевского района Якутской АССР, — 14. 12. 1976, Якутск], якутский советский поэт. Народный поэт Якутской АССР (1964). Член КПСС с 1946. В 1928 окончил Московский институт журналистики. Участник Великой Отечественной войны 1941—45. Автор сборников стихов и поэм «Красные песни» (1925), «Счастливая жизнь» (1938), «Песни победы» (1950), «Негаснущий огонь» (1969), «Сердце друга» (1973) и др. Новизна формы, самобытность, гражданский пафос стихов Э. обусловили влияние его творчества на развитие якутской поэзии. Перевёл произведения А. С. Пушкина, Т. Г. Шевченко, В. В. Маяковского и др. Награжден орденом Октябрьской Революции, 2 другими орденами, а также медалями.
Соч.: Талыллыбыт айымньылар, т. 1—2, Якутскай, 1964—65; Талыллыбыт айымньылар, т. 1—2, Якутскай, 1974; в рус. пер. — Мой хомус, М., 1974.
Лит.: Очерк истории якутской советской литературы, М., 1970.
Элмайра
Элма'йра(Elmira), город на С.-В. США, в штате Нью-Йорк, на р. Шеманг (приток Саскуэханны). 36 тыс. жителей (1975), с пригородами 100 тыс. жителей Металлообрабатывающая и машиностроительная (производство пишущих и счётных машин, конторского и радиоэлектронного оборудования, противопожарной техники), химическая промышленность. Основан в 1788.
Читать дальшеИнтервал:
Закладка:
