БСЭ - Большая Советская энциклопедия (Пр)

Некоторые положения и факты П. г. применяются в номографии, в теории статистических решений, в квантовой теории поля и в конструировании печатных схем (через теорию графов).

Лит.: Вольберг О. А., Основные идеи проективной геометрии, 3 изд., М. — Л., 1949; Глаголев Н. А., Проективная геометрия, 2 изд., М.,1963; Ефимов Н. В., Высшая геометрия, 5 изд., М., 1971; Хартсхорн Р., Основы проективной геометрии, пер. с англ., М., 1970; Veblen О., Young J. W., Projective geometry, v. 1—2, Boston — N. Y., 1910—18.

По материалам одноимённой статьи из 2-го издания БСЭ.

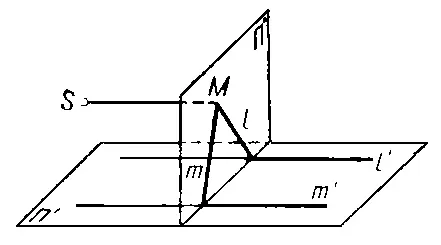
Рис. 1.

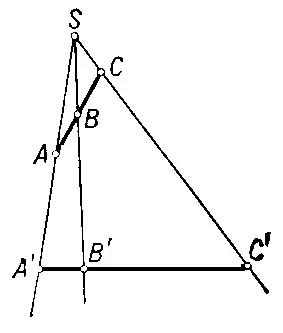
Рис. 2.

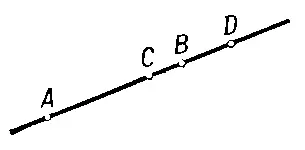
Рис. 3.

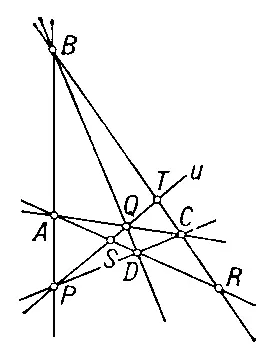
Рис. 5.

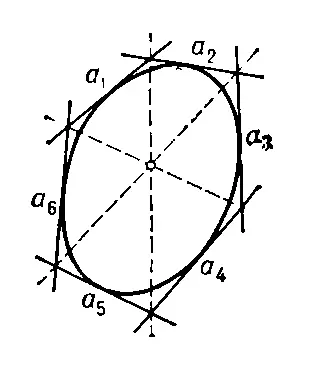
Рис. 7.

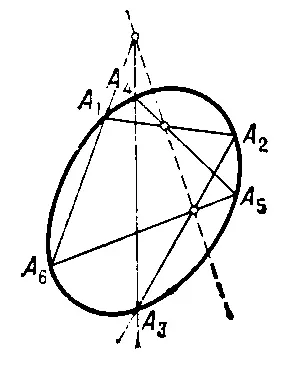
Рис. 6.

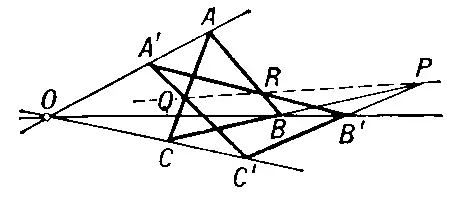
Рис. 4.

Проекти'вная ме'трика, способ измерения длин и углов средствами проективной геометрии . Он состоит в закреплении некоторой фигуры в качестве абсолюта, определяющего данную метрическую геометрию, и выделении из группы всех проективных преобразований таких, которые отображают абсолют в себя и порождают т. о. соответствующую группу движений. Например, метрика плоскости Лобачевского получается, если за абсолют принять нераспадающуюся действительную линию второго порядка,— тогда длина отрезка AB равна l ln ( ABPQ ), где Р и Q — точки пересечения прямой AB с абсолютом, ( ABPQ ) — двойное отношение, l — константа, одинаковая для всех отрезков. Если для измерения длин и углов используется линия второго порядка без действительных точек. то получается (эллиптическая) геометрия Римана. Для построения евклидовой и псевдоевклидовой геометрий выбирают вырожденные линии второго порядка.

Лит.: Ефимов Н. В., Высшая геометрия, 5 изд., М., 1971; Клейн Ф., Неевклидова геометрия, пер. с нем., М. — Л.,1936.

Проекти'вная пло'скость, в первоначальном смысле — евклидова плоскость, дополненная бесконечно удаленными точкамии бесконечно удаленной прямой (см. Проективная геометрия ) . С топологической точки зрения П. п. является замкнутой неориентируемой поверхностью, эйлерова характеристика которой равна 1.

Проекти'вное преобразова'ние, взаимно однозначное отображение проективной плоскости или проективного пространства в себя, при котором точки, лежащие на прямой, переходят в точки, также лежащие на прямой (поэтому П. п. иногда называется коллинеацией). П. п. проективной прямой называется взаимно однозначное отображение её в себя, при котором сохраняется гармоническое расположение точек этой прямой. Простейшим и вместе с тем наиболее важным для приложений примером П. п. является гомология — П. п., оставляющее на месте прямую и точку вне её. Примером П. п. пространства является перспектива, т. е. проектирование фигуры F , лежащей в плоскости П, из точки S в фигуру F' , расположенную в плоскости П' , любое П. п. получается конечной последовательностью перспектив. П. п. образуют группу , основным инвариантом которой является двойное отношение четырёх точек прямой. Теории инвариантов групп П. п., оставляющих на месте некоторую фигуру, представляют собой метрические геометрии (см. Проективная метрика ).

Основная теорема о П. п. проективной плоскости состоит в том, что каковы бы ни были четыре точки А , В , С, D плоскости П , из которых никакие три не лежат на одной прямой, и четыре точки A' , B' , C' , D' той же плоскости, из которых никакие три также не лежат на одной прямой, существует и притом только одно П. п., которое точки А , В , С , D переводит соответственно в точки A' , B' , C' , D'. Эта теорема применяется в номографии и аэрофотосъёмке. Аналогичная теорема имеет место и в проективном пространстве: там П. п. определяется пятью точками, из которых никакие четыре не лежат в одной плоскости. Эта теорема эквивалентна аксиоме Паппа.

В однородных координатах П. п. выражается однородным линейным преобразованием , определитель матрицы которого не равен нулю. Рассматриваются также П. п. евклидовой плоскости или пространства; в декартовых координатах они выражаются дробно-линейными функциями , причём свойство взаимной однозначности утрачивается.

Лит. см . при ст. Проективная геометрия .

Проекти'вное простра'нство, в первоначальном смысле — евклидово пространство, дополненное бесконечно удалёнными точками, прямыми и плоскостью, называемыми также несобственными элементами (см. Бесконечно удалённые элементы ). При этом каждая прямая дополняется одной несобственной точкой, каждая плоскость — одной несобственной прямой, всё пространство — одной несобственной плоскостью; параллельные прямые дополняются общей несобственной точкой, непараллельные — разными; параллельные плоскости дополняются общей несобственной прямой, непараллельные — разными; несобственные точки, дополняющие всевозможные прямые данной плоскости, принадлежат несобственной прямой, дополняющей ту же плоскость; все несобственные точки и прямые принадлежат несобственной плоскости.

П. п. можно определить аналитически как совокупность классов пропорциональных четверок действительных чисел, не равных одновременно нулю. При этом классы интерпретируются либо как плоскости П. п., а числа называются однородными координатами плоскостей. Отношение инцидентности точки ( x 1: x 2: x 3: x 4) и плоскости ( u 1 : u 2: u 3: u 4 ) выражается равенством: 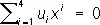. Аналогичнымобразом вводится понятие n -мерного П. п., играющего важную роль в алгебраической геометрии, причём координатами его могут быть элементы некоторого тела k. В более общем смысле П. п. — совокупность трёх множеств элементов, называется соответственно точками, прямыми и плоскостями, для которых определены отношения принадлежности и порядка так, что соблюдаются требования аксиом проективной геометрии . А. Н. Колмогоров и Л. С. Понтрягин показали, что если П. п. над телом k есть связное компактное топологическое пространство, в котором прямая непрерывно зависит от двух принадлежащих ей точек, и выполняются аксиомы инцидентности, то k есть либо поле действительных чисел, либо поле комплексных чисел, либо тело кватернионов.