Питер Макоуэн - Вычислительное мышление: Метод решения сложных задач

Логические вентили не обязательно делать из транзисторов. Как мы видели, их можно создать из простых нейронных контуров. Если заменить логические вентили на основе транзисторов эквивалентами на основе нейронов, результат будет аналогичным. Исследователи в лабораториях электроники и вычислительной техники по всему миру исследуют возможности биокомпьютинга. Например, они наблюдают, как меняется пульсация в нейронных контурах с течением времени, и размышляют, как учесть это в быстрообучающихся кремниевых или германиевых микросхемах. Алгоритмическое мышлениеработает в обе стороны. Оно не только позволяет заниматься научными исследованиями — порой алгоритмические версии природных процессов помогают найти новые способы работы компьютеров.

Наша простая схема подсчета монет, которая учится правильно выполнять задачу с нуля, делает тривиальные операции. Но если такую схему объединить с миллионами похожих для совместной работы, можно создать огромную вычислительную армию. Конечно, самое сложное — запрограммировать ее. Нужно разработать необходимое программное обеспечение, и все они будут вместе работать над общей целью.

Наша игра с проверкой монет была не слишком интересной. Давайте сыграем в настоящую игру — например, «Снап!». Если две карты совпадают, кричите «Снап!». Если они разные, молчите. Чтобы упростить процесс, будем считать, что у нас есть только красные и черные карты. Получится ли создать нейронную сеть, чтобы сыграть в эту игру?

Давайте разберем, как именно наша нейронная сеть будет определять совпадение цветов. Пусть 1 означает карту красного цвета, а 0 — черного. Красный–красный (1, 1) или черный–черный (0, 0) — это «Снап!», красный–черный (1, 0) или черный–красный (0, 1) — нет. Процесс похож на проверку монет с помощью И, но не так прост в освоении.

Цветной «Снап!» — это пример использования функции исключающее ИЛИ. Она немного похоже на функцию И, но активизируется, только если на входе (1, 0) или (0, 1), — и ни в каких иных случаях. Функция активизируется, только если истине соответствует один сигнал (то есть один сигнал равен 1), но не оба, как на рис. 48.

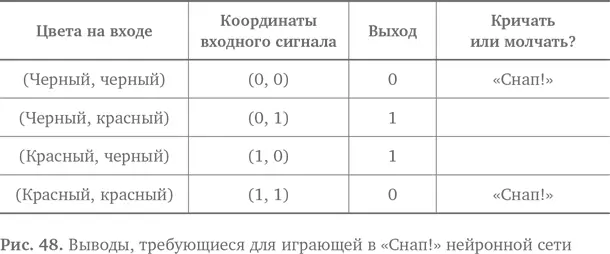
На заре нейронных сетей такого рода логика представляла собой большую проблему. Нейронные контуры, которые тогда назывались перцептронами,отлично работали с И, ИЛИ и с другими простыми операциями в булевой логике, но не могли справиться с досадным моментом исключения. Причина состояла в их геометрии. Оказалось, что перцептрон работал, создавая границу решения — линию на графе. При достаточном сигнале на вводе перцептрон переходил через границу. Это зависело от весов и порогов восприятия в контуре (наши значения И1, И2 и Д в предыдущей игре). Пока явления, для которых мы хотели получить разный выход, были по разные стороны границы решения, все было хорошо — перцептрон работал.

Но в случае с функцией «исключающее ИЛИ», где нам нужна линия в соответствии с таблицей на рис. 48, ничего не получилось. Если изобразить это на графе с использованием данных координат (где красный — 1, а черный — 0), то окажется, что на выходе невозможно отделить ответы, равные 0, от ответов, равных 1. Нельзя создать систему, в которой, когда вас толкают через границу, одно состояние сменяется другим (см. рис. 49).

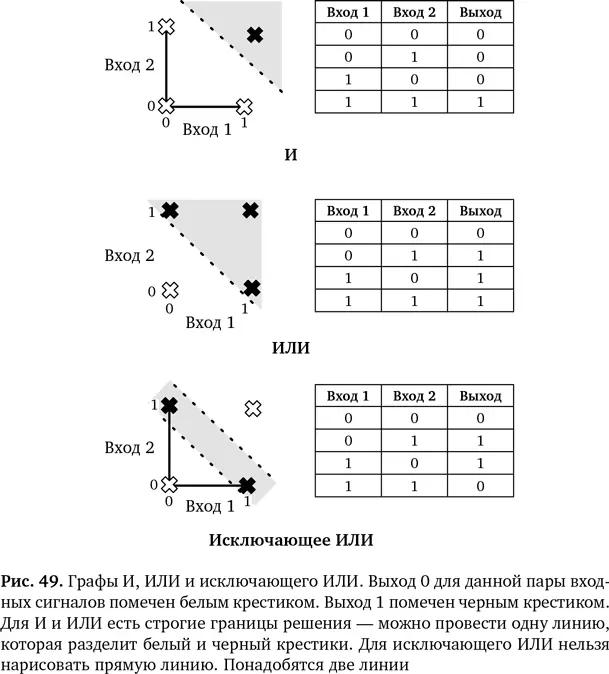
И вот идея: если каждый перцептрон может нарисовать только одну линию, нужно использовать больше перцептронов. Если один перцептрон будет питать другой и получится так называемый многослойный перцептрон,то каждый слой будет определять линию решения и мы сможем использовать две линии.

Да, сделать его можно. Есть несколько способов создать нейронные контуры, которые могут работать с исключающим ИЛИ или играть в «Снап!», и на рис. 50 представлен один из таких способов. Заметим, что здесь мы используем представлениев виде графа,чтобы показать нейронный контур. В конечном итоге главное здесь — нейроны и их взаимосвязи. Еще мы абстрагируемсяот внутренних подробностей работы нейронов и сосредотачиваемся на их усвоенном поведении.

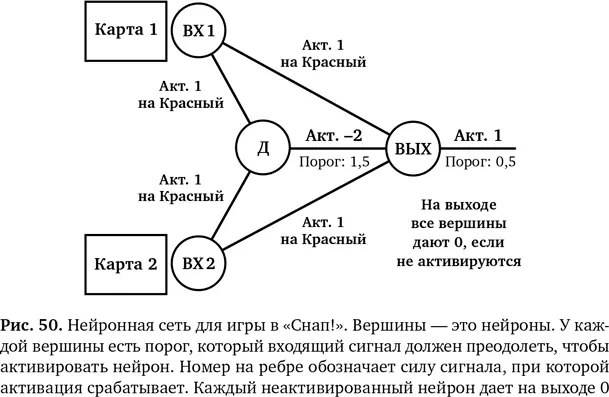
Теперь у нас есть нейронная сеть из четырех взаимосвязанных нейронов. У нас два нейрона на входе — ВХ1 и ВХ2, которые определяют цвет видимых ими карт. Они дадут на выходе 1, если карта красная, и 0 — если черная. Этот результат идет в нейрон Д (дом) во втором слое. Порог для его активации — 1,5 (то есть он активируется при условии, что сумма сигналов на входе больше 1,5), но сам он дает на выходе отрицательный результат ( −2). Все сигналы поступают в третий нейрон, ВЫХ с порогом 0,5.

Эту схему нужно проверить. Давайте пройдемся по всем комбинациям.

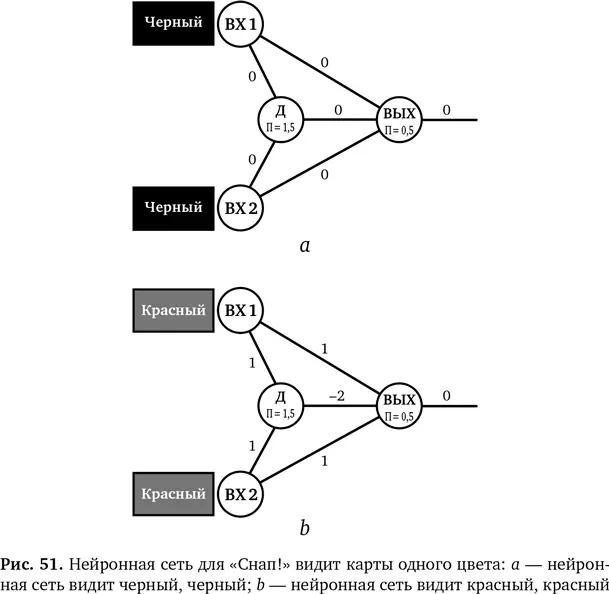
Если на входе поступает комбинация (0, 0), это (черный, черный), и нейрон во втором слое, Д, получает сигнал 0 с обеих сторон (см. рис. 51 a). Для Д сигнал 0 меньше, чем порог 1,5, поэтому вершина Д активирует 0. Сигналы, поступающие на нейрон ВЫХ, суммируются (0 + 0 + 0), и на выходе Д дает 0. Это меньше, чем порог 0,5 для нейрона ВЫХ, поэтому он не активируется, и перцептрон на выходе дает 0.

Комбинация (красный, красный) дает на вход в нейрон Д (1 ,1), в сумме 2. Это больше, чем 1,5, поэтому Д активируется и дает на выходе –2. На ВЫХ у нас есть сигналы, поступающие напрямую со слоев входа, 1 и 1, поэтому их надо добавить к взвешенному сигналу –2 от Д: (1 + 1 + ( –2)). В сумме получается 0, и это меньше, чем порог для ВЫХ, поэтому на выходе получается 0 (рис. 51 b).

Если на вход поступает сочетание (0, 1), то есть (черный, красный), то Д получает только 1, что меньше его порога, поэтому Д не активируется. На ВЫХ мы получаем 0 от ВХ1, поскольку на входе черный, и 1 от ВХ2, потому что на другом входе — красный. Они суммируются с 0 на Д (0 + 1 + 0) и дают 1. Это больше, чем 0,5, поэтому на выходе происходит активация — ВЫХ выдает 1 (см. рис. 52 a).

Рассмотрите последний случай, где на входе (1, 0), то есть (красный, черный), и вы увидите, что на ВЫХ будет 1, как на рис. 52 b.

В целом эта закономерность сочетаний на входе и на выходе соответствует таблице для исключающего ИЛИ. А чтобы правильно играть в нашу игру, нужна именно она. Таким образом, мы создали элементы мозга, которые умеют играть в цветной «Снап!».