Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

Третье и четвёртное ограничения означают, что при фиксированном значении одного из факторов последовательное увеличение другого фактора будет приводить к сокращению прироста значения Q .

Пятое и шестое ограничения означают, что каждый из факторов производства необходим в том смысле, что если один из факторов равен нулю ( K=0 или L=0 ), то и объём производства также равен нулю Q=0 .

Двухфакторную производственную функцию Кобба-Дугласа f(K,L) можно представить в виде:

Q=A*Ka*Lβ,

где Q – объём выпущенной продукции (в стоимостном или натуральном выражении);

K – объём основного капитала или основных фондов;

L – объём трудовых ресурсов или трудовых затрат (измеряемое количеством рабочих или количеством человеко-дней).

A, a, β – неизвестные числовые параметры производственной функции, которые подчиняются условиям:

1) 0≤а≤1;

2) 0≤β≤1;

3) A›0;

4) a+β=1.

Данная производственная функция характеризуется следующими показателями:

1) частный коэффициент эластичности производственной функции Кобба-Дугласа по факторной переменной капитала K рассчитывается по формуле:

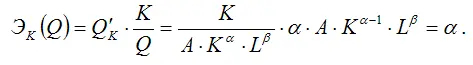
Таким образом, ЭК(у)=а, т. е. частный коэффициент эластичности функции Кобба-Дугласа равен числовому параметру а , и, следовательно, является независимым от переменных К и L ;

2) частный коэффициент эластичности производственной функции Кобба-Дугласа по факторной переменной затрат труда L рассчитывается по формуле:

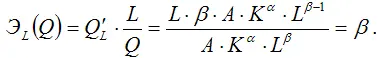
Таким образом, ЭL(у)=β , т. е. частный коэффициент эластичности функции Кобба-Дугласа равен числовому параметру β , и, следовательно, является независимым от переменных К и L ;

3) коэффициент средней производительности труда производственной функции Кобба-Дугласа:

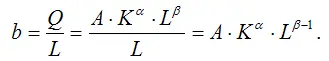
4) коэффициент средней фондоотдачи производственной функции Кобба-Дугласа:

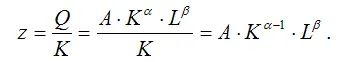
5) коэффициент предельной производительности труда производственной функции Кобба-Дугласа:

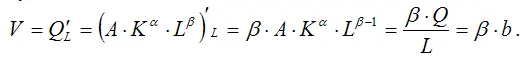
Данный показатель характеризует величину эффекта от каждой дополнительной единицы затраченного труда. Он пропорционален показателю средней производительности труда, но всегда меньше его величины, т. к. 0≤β≤1 ;

6) коэффициент предельной фондоотдачи производственной функции Кобба-Дугласа:

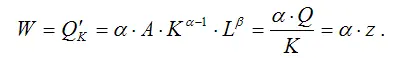
Данный показатель характеризует величину эффекта от каждой дополнительной единицы основных фондов, использованной в производстве. Он пропорционален показателю средней производительности, но всегда меньше его величины, т. к. 0≤а≤1 ;

7) коэффициент предельной нормы технической замены факторных переменных (замены труда капиталом) производственной функции Кобба-Дугласа:

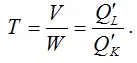
Данный показатель характеризует, на сколько единиц можно уменьшить объём используемого капитала при увеличении объёма трудовых затрат на единицу и фиксированном объёме выпуска продукции.

Двухфакторную производственную функцию Кобба-Дугласа f(K,L) можно представить в виде:

Q=A*Ka*Lβ,

где Q – объём выпущенной продукции (в стоимостном или натуральном выражении);

K – объём основного капитала или основных фондов;

L – объём трудовых ресурсов или трудовых затрат (измеряемое количеством рабочих или количеством человеко-дней).

A,a,β – неизвестные числовые параметры производственной функции, которые подчиняются условиям:

1) 0≤а≤1;

2) 0≤β≤1;

3) A›0;

4) a+β=1.

Двухфакторная производственная функция Кобба-Дугласа относится к классу нелинейных по параметрам функций, которые можно свести к линейному виду.

Для того, чтобы привести двухфакторную производственную функцию Кобба-Дугласа к линейному виду, необходимо прологарифмировать обе части данной функции:

lnQj–lnLj=lna+β(lnKj–lnLj)+εj, ,

где εj – случайная ошибка производственной функции

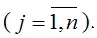
Для более наглядного представления данной модели регрессии воспользуемся методом замен:

yj= lnQj–lnLj;

b0=lna;

b1=β;

b=[ b0 b1]T;

xj= lnKj–lnLj;

δT(xj)=[0 xj].

В результате произведённых замен получим окончательный вид производственной функции Кобба-Дугласа, приведённой к линейной форме:

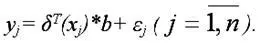
В данной функции неизвестным является только вектор коэффициентов b. Оценку данного вектора можно получить с помощью классического метода наименьших квадратов по формулам:

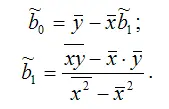
где

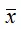
– среднее арифметическое значение переменной х :

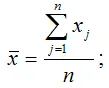
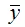
– среднее арифметическое значение переменной у :

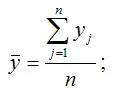
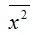
– среднее значение квадрата переменной х :

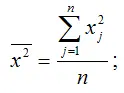
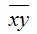
– среднее значение произведения переменных х и у :