Друнвало Мельхиседек - Древняя Тайна Цветка Жизни. Том 1

Леонардо нарисовал эти маленькие линии, составляющие сетку поверх и вокруг тела (Рис.7-43): в центре находятся четыре квадрата (А, В, С и D) и восемь квадратов, которые их окружают (от Е до L). Эти внешние восемь квадратов оказываются там, где восемь полудиагоналей Рис.7-41 пересекают тело и откуда начинаются восемь спиралей (Рис.7-42). Таким образом, вокруг тела расположены восемь точек и центральная модель, состоящая из четырёх квадратов – в середине, и всё это сосредоточено в точности вокруг первоначальных восьми клеток. Жизнь удивительна, не правда ли?

Когда я заметил это на рисунке Леонардо, я решил, что в этом взаимоотношении должно быть что-то важное. Но когда я понял, что в природе не существует такого явления, как прямоугольник или спираль Золотого Сечения, я начал подозревать, что эти спирали, вероятно, чем-то слегка отличаются. Так оно и оказалось – они слегка отличаются.

Оказывается, что эти спирали являются спиралями Фибоначчи в природе, и это мы исследуем в следующей главе. Понимание различия между Золотым Сечением и сечением Фибоначчи может показаться простым и неважным – до тех пор, пока не проявится более широкая картина природы, раскрывающая относительно этой взаимосвязи нечто поразительное. Не зная этого различия, никто никогда не сможет понять, почему на Земле были выстроены эти 83 тысячи священных места и каково их назначение.

Для того, чтобы понять, почему эти восемь спиралей вокруг Канона да Винчи не являются спиралями Золотого Сечения, и для понимания того, что же они собой представляют, мы должны обратиться к другому человеку – не Леонардо да Винчи, но Леонардо Фибоначчи. Фибоначчи жил лет на 250 раньше да Винчи. Согласно тому, что я о нём читал, он был монахом и часто пребывал в состоянии медитации. Он любил прогуливаться по лесам и медитировать во время прогулок. Но его левое полушарие мозга явно было в это время активно, потому что он начал замечать, как растения и цветы содержат в себе числовые соответствия (Рис.8-1).

Схемы, по которыми сформированы лепестки, листья и семена цветов, соответствуют определённым числам, и в этом списке должны значиться цветы, которые, если я правильно уловил, я думаю, он видел на своих прогулках. Он заметил, что лилии и ирисы имеют по три лепестка, а лютики, живокость и водосбор (цветок в верхнем правом углу на Рис.8-1) – по пять. Некоторые шпорники имеют по 8 лепестков, ноготки имеют 13, некоторые астры же – 21 лепесток. Маргаритки почти всегда имеют 34, 55 либо 89 лепестков. Эти же самые числа начали встречаться ему всюду в природе, опять и опять.

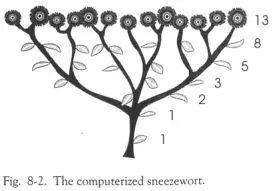
Это маленькое растение (Рис.8-2) на самом деле не существует; мы создали его с помощью компьютерной графики, тасуя данные, как колоду карт. Подлинное растение, на котором основана эта иллюстрация, называется трава-чихун (тысячелистник птармика); мы просто составили на компьютере графическое изображение этого растения.

Фибоначчи заметил, что когда росток травы-чихун только появляется из земли, на нём вырастает только один лист, всего один маленький листик. Затем он немного вытягивается, и на стебле вырастает ещё один листок, потом немного дальше у него вырастает два листа, потом три, затем пять и затем – восемь; после этого он выбрасывает тринадцать соцветий. Вероятно, он подумал: «Эй, это те же самые числа, которые я вижу всюду в лепестках у других цветов – 3, 5, 8, 13.»

В конце концов, эта последовательность из чисел 1, 1, 2, 5, 8, 13, 21, 34, 55, 89 и так далее стала известна как последовательность Фибоначчи . Если вам известны любые три последующих числа из этой последовательности, то вы можете распознать всю закономерность: остаётся лишь сложить два последовательных числа, чтобы получить число, следующее за ними. Видите, как это работает? Это совершенно особенная последовательность. В жизни она является решающей. Пожалуй, это будет моей интерпретацией пояснения причины, по которой она является ключевой, но я изо всех сил постараюсь вам показать.

Это – пятилепестковый цветок гибискуса (Рис.8-3). Тычинка внутри оканчивается пятью почками, и направление этих двух геометрических форм противоположно друг относительно друга, одна группа устремлена вверх, другая направлена вниз. Большинство людей, глядя на этот цветок, не думают: «Гляди-ка, у него пять лепестков». Они просто смотрят на него, замечают его красоту, нюхают его и воспринимают его правым полушарием своего мозга. Они не думают о геометрии или метаматике – о том, что происходит на другой стороне мозга.

Как жизнь разрешила вопрос бесконечной спирали Золотого Сечения (Ф)

Помните, я сказал, что спираль Золотого Сечения не имеет ни начала, ни конца, и что у жизни возникли с этим большие проблемы? С отсутствием конца она ещё может иметь дело, но совсем не просто сладить с чем-то, не имеющим начала. Мне действительно трудно с этим сладить и я думаю, с этой ситуацией мы боремся все.

Чтобы обойти эту проблему, природа создала последовательность Фибоначчи. Это подобно тому, как если бы Бог сказал: «Окей, ступайте и творите по спирали Золотого Сечения», а мы возразили: «Мы не умеем». И тогда мы создали нечто, не являющееся спиралью Золотой Середины, но так быстро к ней приближающееся, что отличие становится едва различимо

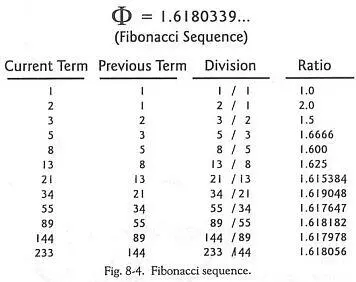
Например, пропорция Ф, связанная с Золотым Сечением, приблизительно равна 1,6180339. Смотрите, что происходит, когда вы делите каждое число в последовательности Фибоначчи на последующее. В левой колонке дана последовательность: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89. В следующей колонке я сдвинул последовательность на одно число, так, чтобы мы могли на одной строчке разделить число в первой колонке на число во второй колонке (см. колонку 3). Обратите внимание, что происходит, когда вы делите число из первой колонки на число из второй колонки. При делении 1 на 1 мы получаем 1,0. Теперь: 1,0 значительно меньше пропорции Ф. Но перейдя на следующую строчку, и разделив 2 на 1, мы получаем 2, что больше Ф, но ближе к нему, чем 1. Разделив 3 на 2, мы имеем 1,5 что значительно ближе к Ф, нежели предыдущие два результата, но этого ещё мало. 5 поделенное на три даёт результат 1,6666, что больше искомого, но к нему значительно ближе. 8, поделенное на 5, даст 1,60 – это меньше Ф. Поделенное на восемь 13 даёт 1,625, это больше. Поделив 21 на тринадцать, получаем 1,615 – меньше. Разделив 34 на 21, получаем 1,619, что – больше. Разделив 55 на 4, получаем 1,617 – меньше. Поделим 89 на пятьдесят пять, это будет 1,6181 – больше. Следующий результат будет немного меньше, потом будет больше, и так каждый раз, приближаясь всё ближе и ближе к действительной пропорции Ф. Это называется асимптотическим приближением к пределу. Достичь самого числа вообще никогда невозможно, но и заметить разницу после нескольких делений тоже становится практически невозможно. Графически это можно увидеть на Рис.8-5.