Друнвало Мельхиседек - Древняя Тайна Цветка Жизни. Том 1

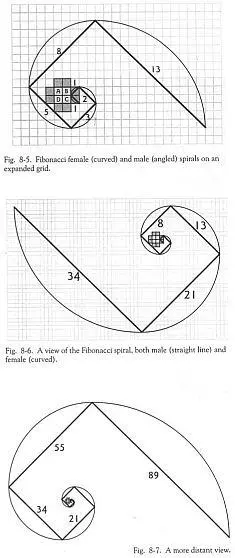
Светлосерые квадраты – это четыре центральных квадрата тела человека, где расположены восемь первоначальных клеток. Восемь тёмносерых квадратов вокруг этих центральных квадратов – это те, где начинаются спирали. Все в этом разобрались?

Вместо того, чтобы позволить спирали бесконечно закручиваться, мы поступим иначе – потому что, на мой взгляд, так поступает жизнь. В качестве исходной точки я воспользуюсь одним из внешних квадратов, и это будет справедливо для всех восьми квадратов. Я выбираю один из них в качестве примера.

Воспльзовавшись диагональю, проведенной через всего лишь один крошечный квадрат фона, как меркой, назовём эту линию диагонали одной единицей. Затем будем двигаться в соответствии с числами Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 89, совершая поворот откладываемой линии после каждого числа на 90°. Сначала мы откладываем одну длину, затем поворачиваемся на 90° и откладываем ещё одну длину. Потом делаем поворот на 90° и продвигаемся на две длины, следующий поворот на 90° и -продвижение по прямой на три длины. Перед каждым продвижением мы совершаем поворот на 90°. Следующий шаг имеет длину в 5 единиц, потом следует 8. Таким образом мы получаем отрезки длиной 1, 1, 2, 3, 5, 8, 13.

Затем мы пересекаем по диагонали 21 квадрат, а потом 34 (Рис.8-6). Потом следуют 55 и 89 (Рис.8-7) Проделывая это, спираль разворачивается и всё ближе и ближе подходит к Ф, спирали Золотого Сечения, до тех пор, пока в жизни становится уже практически невозможно определить разницу, по крайней мере визуально.

Сравнение двух спиралей должно быть очень важным действием при изучении жизни, потому что древние Египтяне показали в Великой Пирамиде как спираль Фибоначчи, так и спираль Золотого Сечения. Несмотря на то, что эти спирали имеют два различных источника, к тому моменту, как они достигают ступеней 55 и 89, две их линии становятся практически идентичными. Когда люди, изучавшие Египет, увидели, что три пирамиды выстроены по спирали, они подумали, что это спираль Золотого Сечения, а не спираль Фибоначчи. Затем они вернулись и обнаружили одну из ямок (см. Главу 4, подзаголовок Как была построена сетка и где ). Спустя несколько лет стало ясно, что совсем недалеко, может быть, ярдах в ста или около того, была ещё одна метка. Они не поняли, что спиралей было две. Я не знаю, понимают ли сейчас люди, работающие с этим, насколько это важно.

Спирали в природе

Вот священная геометрия в природе (Рис.8-8), подлинное явление. Это срез раковины моллюска наутилуса. Существует неписаное правило, что каждая хорошая книга по священной геометрии должна содержать в себе раковину наутилуса. Многие книги утверждают, что это спираль Золотого Сечения, но это не так – это спираль Фибоначчи.

Можно увидеть совершенство рукавов спирали, но если посмотреть в центр или начало, то она не выглядит так идеально. Здесь эта деталь действительно неразличима. Я предлагаю вам рассмотреть подлинник. В дествительности, внутренний конец спирали выходит на другую сторону и изгибается коленом, потому что его длина равна 1, что очень далеко от Ф. Второе и третьее колено тоже изгибаются, но не настолько, потому что они больше приближены к Ф. Затем соответствие становится всё большим и большим, до тех пор, пока вы не увидите, как эта изящная форма разворачивается. Вы могли бы решить, что этот маленький наутилус в начале совершил ошибку; кажется, будто там он ещё не знал, что он делает. Но он выстроил всё идеально, без ошибок. Он просто точно следовал математике последовательности Фибоначчи.

На этой сосновой шишке (Рис.8-9) вы видите двойную спираль, одна движется в одном, а другая в другом направлении. Если бы вы посчитали число витков спирали, вращающейся в одном направлении, а затем – в другом, то обнаружили бы, что это будут всегда два последовательных числа Фибоначчи. Возможно, это 8 оборотов в одном направлении и 13 в другом, или 13 в одном направлении, и 21 – в другом. Многие другие двуспиральные модели, находимые всюду в природе, соответствуют этому закону во всех известных мне случаях. Например, спирали подсолнуха всегда привязаны к последовательности Фибоначчи.

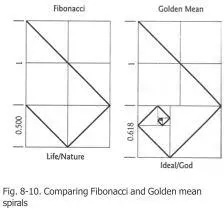
Рис. 8-10 показывает различие между двумя спиралями. Спираль Золотого Сечения идеальна. Она подобна Богу, Источнику. Как видите, верхние четыре квадрата на обоих рисунках -одинакового размера. Различие – в областях, где они получают начало (нижние отделы двух диаграмм). Область нижней части спирали Фибоначчи равна половине (0,5) области её верхней части; область нижней части спирали Золотого Сечения равна 0,618 области её верхней части. Спираль Фибоначчи, показанная на Рис.8-10 выстроена при помощи шести равных квадратов, в то время как спираль Золотого Сечения начинается глубже внутри (в действительности, она вообще никогда не начинается – она длится вечно, как Бог). Хотя исходные точки спиралей различны, их линии начинают очень быстро сближаться.

Другой пример: множество книг утверждает, что Царская Палата представляет собой прямоугольник Золотого Сечения, но это не так. Это опять связано с Фибоначчи.

Спирали Фибоначчи вокруг Людей

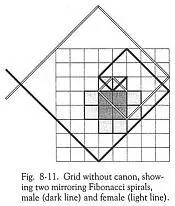
Начертив сетку в 64 клетки и объединив эту спиральную модель, мы получаем Рис.8-11.

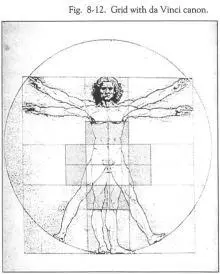
Наложив канон да Винчи на эту сетку восемь-на-восемь (Рис.8-12), мы обнаруживаем, что восемь заштрихованных клеток обладают уникальным свойством. Существует восемь возможных способов выведения спирали Фибоначчи из четырёх спаренных клеток. Давайте вернёмся к Рис.8-11 и воспользуемся верхними спаренными клетками как примером. Один способ начать, это – с верхнего правого угла, как показано чёрной линией. Она пересекает одну клеточку (1), поворачивает направо, чтобы пересечь ещё одну клетку (1), поворачивает направо ещё раз для пересечения двух клеток (2) – довольно интересно то, что в этой точке она достигает верхней линии данной сетки. Продолжая поворачивать направо, она пересекает 3 клетки (следующее число в этой последовательности) и – подумать только! – теперь она коснулась правой стороны сетки! Следующее число – 5 – приводит нашу линию к нижнему краю сетки. Потом будет число 8. И прежде, чем покинуть сетку, линия спирали пройдёт через три клетки. Число 8 проводит линию через три клетки перед тем, как покинуть сетку. По мере развертывания спирали из начальной клетки, прослеживается идеальное рефлективное качество зеркального отражения.