Сергей Доронин - Квантовая магия

Более подробное рассмотрение основного разложения матрицы плотности целесообразно начать с самого простого случая двухуровневой системы (кубита). Напомню также, что все матрицы плотности — эрмитовы.

В матричном анализе доказывается утверждение, что всякую эрмитовуматрицу 2 × 2 можно однозначно записать в виде вещественной линейной комбинации единичной матрицы и трех матриц с нулевым следом, так называемых матриц Паули, в частности, любая матрица плотности 2 × 2 представляется в виде:

ρ = 1/2 ( Е + ασ x + βσ y + γσ z ),

где Е — единичная матрица, α, β, γ — вещественные числа, а σ x , σ y и σ z — матрицы Паули [см. (3.12)]. Мы уже пользовались такой формой записи в выражении (3.11).

Этот результат для матриц 2 × 2 является частным случаем хорошо известного в квантовой теории общего утверждения, что любая матрица плотности произвольной размерности может быть записана в виде [98]:

ρ ε= (1 — ε) M d + ε ρ 1, (3.14)

где d = 2 N — размерность гильбертова пространства системы, состоящей из N подсистем; M d = 1 d/d — максимально смешанное состояние (нормализованная единичная матрица плотности, след которой равен 1); 1 d— единичная матрица размерностью d; ρ 1— произвольная матрица плотности; ε — вещественный параметр (0 ≤ ε ≤ 1).

В форме (3.14) часто анализируют псевдочистыесостояния [99], когда ρ 1= | ψñá ψ|.

ρ ε= (1 — ε) M d + ε| ψñá ψ|.

Выражение (3.14) можно переписать в виде:

ρ ε= M d + ε( ρ 1— M d ). (3.15)

То есть любая матрица плотности может быть представлена в виде суммы матрицы максимально смешанного состояния M d (с единичным следом) и матрицы с нулевым следом ( ρ 1— M d ), напомню, что след у ρ 1тоже равен единице.

Таким образом, состояние произвольной системы имеет двуединую природу, содержит в своей структуре две качественно различные составляющие: одна часть неизменная, вечная (максимально смешанное состояние), и вторая часть динамическая (если система динамическая, параметр ε может быть, например, функцией времени).

Рассмотрим более детально, что такое максимально смешанное состояние. Наверное, это будет легче понять на примере кубита. Только для начала мы запишем вектор состояния кубита | ψñ = a |0ñ + b |1ñ в виде нужной матрицы плотности. Этот вектор состояния зависит от четырех вещественных параметров ( a и b — комплексные числа). Число параметров можно уменьшить до двух, воспользовавшись двумя дополнительными условиями, налагаемыми на вектор состояния, — условием нормировки | a | 2+ | b | 2= 1 и одним из постулатов квантовой механики, согласно которому состояния не меняются, если их умножить на фазовый множитель exp(± iφ ). То есть,например, состояния |0ñ и exp( iφ ) |0ñ тождественны. Это следствие того факта, что модуль комплексной экспоненты равен единице.

Следовательно, необходимы лишь два независимых вещественных параметра, чтобы однозначно задать вектор состояния кубита. Обычно в качестве таких параметров выбирают два угла θ и φ , которые однозначно определяют точку на сфере Блоха (см. рис. 1). В этом случае

a = exp(— iφ /2) cos( θ /2)

b = exp( iφ /2) sin( θ /2),

а вектор состояния записывается в виде:

|ψñ = exp(— iφ /2) cos( θ /2) |0ñ + exp( iφ /2)sin( θ /2) |1ñ. (3.16)

Матрица плотности ρ тогда равна сумме двух матриц ρ 1и ρ 2:

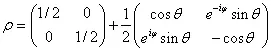. (3.17)

Нам еще пригодится вектор состояния

|ψñ = cos( θ /2) |0ñ+sin( θ /2) |1ñ, (3.18)

и соответствующая ему матрица плотности:

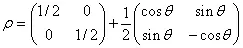. (3.19)

Можно заметить, что (3.16) получается из (3.18) унитарным преобразованием

,

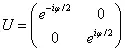то есть чистым вращением вектора состояния (3.18), которое характеризуется параметром φ . Несложно определить, в чем состоит физическое отличие векторов состояния (3.16) и (3.18). Они связаны соотношением | ψñ rot = U | ψñ, которое означает переход между неподвижной и вращающейся системой координат. То есть вектор ( 3.18)мы записали для внутреннего состояния системы — он описывает то, что происходит с точки зрения самой системы. Система «чувствует», что она переходит из одного состояния в другое, и никаких других изменений для нее не существует. Это вид «изнутри» системы. В этом случае ее вектор состояния характеризуется лишь одним вещественным параметром θ . Можно предположить, что это собственное внутреннее время системы, то есть параметр, с которым меняется ее внутреннее состояние.

А состояние (3.16) описывает эволюцию системы в лабораторной (неподвижной) системе координат, связанной с внешним наблюдателем. Это вид «снаружи». Можно пояснить данный момент еще следующим образом. При эволюции системы вектор состояния при любом его положении остается для самой системы осью квантования. Но для внешнего наблюдателя, со своей системой отсчета и выбранной уже им осью квантования (обычно за нее принимают ось Z ), вектор состояния будет перемещаться по сфере Блоха и поворачиваться на угол φ.

Максимально смешанное состояние [первая матрица в правой части выражений (3.17) или (3.19)] определяет две важные характеристики системы. Во-первых — центр сферы Блоха, то есть точку, равную сумме диаметрально противоположных точек, в которых вектор состояния «протыкает» сферу Блоха в любом из своих положений [100], — это ядро, центр системы, из которого выходит сам вектор состояния. Во-вторых, максимально смешанное состояние задает ось квантования, поскольку составляет на этой оси постоянный и неизменный отрезок между двумя (для кубита) точками. Переходя в систему отсчета, связанную с вектором состояния (во вращающуюся систему координат), этот вектор становится осью внутреннего мира системы, на которую с равной вероятностью, с равной возможностью реализации «нанизаны» все допустимые состояния системы. В нашем простейшем случае это два допустимых состояния, которые всегда остаются в распоряжении системы, в каком бы положении ни находился вектор состояния. Но они существуют только как потенциальные возможности, а конкретная реализация той или иной альтернативы зависит уже от динамической части матрицы плотности.

Если рассматривать кубитв качестве элементарного сознания, то его внутреннюю «ось мира», то есть матрицу плотности

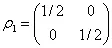, (3.20)

можно назвать простейшей духовной монадой элементарного сознания, поскольку это «неуничтожимая» часть сознания.