Сергей Доронин - Квантовая магия

Но есть и объективные факты — результаты экспериментов, их теоретическое осмысление и выводы, которые невозможно игнорировать, хочешь — не хочешь, но их придется раскладывать «по полочкам». Все равно придется выстраивать непротиворечивую согласованную модель окружающей нас реальности, поскольку уже сейчас очевидно, что те результаты, которые получены, не укладываются в рамки общепринятых представлений. Работа эта длительная и трудная, она потребует совместных усилий многих и многих специалистов. Мы пока находимся в самом начале этого процесса, но фундамент уже заложен, и на него уже можно опереться.

Возможно, все эти заявления кому-то покажутся чересчур преувеличенными. Не исключаю, что сомнения могут быть вызваны тем обстоятельством, что у многих квантовая физика вызывает лишь смутные ассоциации с чем-то очень далеким от нашей повседневной жизни, с тем, что никоим образом не затрагивает наш внутренний мир с его ценностями и предпочтениями. Дескать, пусть над этими вопросами ломают голову ученые и придумывают новые устройства, полезные в повседневной жизни. Однако фундаментальные выводы квантовой теории касаются каждого из нас — причем уже не просто как потребителя «новых технологий», но и на более глубоком, философском уровне, поскольку коренным образом меняют наш взгляд на окружающую реальность. Квантовая теория помогает переосмыслить свои жизненные ценности и глубже понять, в чем заключается смысл нашего земного пути. В свете последних научных результатов жизнь в физическом теле предстает уже не в качестве самодостаточнойценности, а как небольшой этап нашей эволюции в совокупной Квантовой Реальности, как часть Большого Пути, который имеет свое продолжение на других, квантовых ее уровнях.

В дифференциальной геометрии 1-форма определяется как линейная вещественная функция векторов, то есть является линейным оператором, «машиной», на вход которой подаются векторы, а на выходе получаются числа. Простейшей 1-формой является градиент d f функции f (обозначение dили grad обычно используют применительно к скалярным величинам, а Ñ (читай: «набла») — к векторам или тензорам). Внешняя производная, или градиент, является более строгой формой понятия «дифференциал». В отличие от дифференциала df , который выражает изменение f в некотором произвольном направлении, градиент характеризует изменение функции в определенном направлении, заданном бесконечно малым вектором смещения v. Если быть более точным, градиент d f представляет собой совокупность поверхностей уровня f a = const и характеризует их «близость» друг к другу, плотность «упаковки» в элементарном объеме в направлении v, с точностью до приближения их плоскостями и размещения через равные промежутки (вследствие линейности оператора). Результатом пересечения d f вектором смещения vявляется число á d f , vñ = ∂ v f . Это выражение определяет связь между градиентом d f и производной по направлению ∂ v f . Введя вектор vв линейную машину d f , на выходе мы получаем ∂ v f — число пересеченных плоскостей при прохождении vчерез d f , число, которое придостаточно малом vравно приращению f между основанием и острием вектора v.

Задание 1-формы в данной точке (связь с точечным описанием) для некоторого геометрического объекта, описывающего физическую величину, например, для тензора произвольного ранга (0-ранг — скаляр, 1-ранг — вектор или 1-форма, 2-ранг — тензор второго ранга и т. д.), предполагает выполнение трех основных операций. Это, прежде всего, задание вектора смещения, в направлении которого данный объект меняется от точки к точке. Во-вторых: моделирование исходного объекта в окрестностях каждой точки в виде плоских поверхностей уровня, расположенных на одинаковых расстояниях. Инаконец, подсчет числа пересечений этих плоскостей вектором смещения. Поскольку образование 1-формы (градиента) от произвольного тензора предполагает одновременное задание вектора смещения, появляется дополнительный входной канал, и ранг исходного тензора увеличивается на единицу.

Таким образом, дифференциальная геометрия дает более строгое определение градиента в качестве 1-формы, в отличие от обычных представлений градиента как вектора. Градиент, который нам более знаком, — это всего лишь вектор, поставленный в соответствие 1-форме градиента с помощью уравнения (которое уже приводилось) 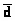f · v= á d f , vñ, где слева стоит скалярное произведение двух векторов, и 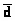f — градиент в виде вектора.

Дифференциальная геометрия расширяет также понятие тензора. Если обычно под тензором понимается линейный оператор с входными каналами для векторов и выходными данными либо в виде вещественных чисел, либо в виде векторов, то теперь во входной канал может подаваться не только вектор, но и 1-форма.

В качестве примера рассмотрим координатное представление тензора второго ранга. В отличие от обычного вектора, который может быть разложен лишь в одном произвольном базисе из ортонормированных векторов (поэтому его можно считать тензором первого ранга), тензор второго ранга разлагается на компоненты в двух базисах. В качестве любого из этих базисов (или обоих сразу) могут служить либо наборы из обычных базисных векторов e α, либо совокупность так называемых базисных 1-форм w α= d x α. Базисные 1-формы — это координатные поверхности x α = const. Следовательно, базисный вектор e αпересекает только одну поверхность базисной1-формы w α(перпендикулярную e α).

Точно так же, как произвольный вектор можно разложить по базису e α, v= ν α e α, произвольную1-форму можно разложить по базису w β, σ = σ β w β. Коэффициенты ν αи σ βназываются компонентами вектора vи 1-формы s в базисе e αи w βсоответственно.

Вводя в некоторый тензор второго ранга Sпроизвольные вектор vи 1-форму σ и, зная компоненты их разложения в своих базисах, через них можно выразить компоненты самого тензора S( v, σ) = S( e α, w β) v ασ β= S α β v ασ β.

Вектор состояния — полное описание замкнутой системы в выбранном базисе. Задается лучом гильбертова пространства.

Волновая функция (волновой вектор) — частный случай вектора состояния, одно из координатных его представлений, когда в качестве базиса выбираются пространственно-временные координаты.