Ренна Шессо - Математика для мистиков. Тайны сакральной геометрии

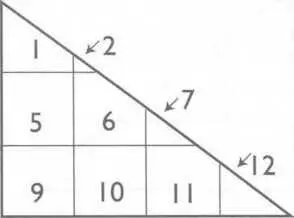
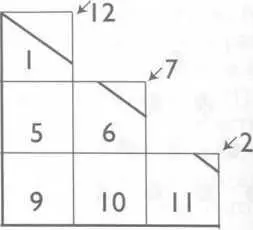
Рис. 73. Разрезанная фигура с рисунка 72. Треугольник Пифагора, переделанный так, чтобы показать, что он равен шести квадратам

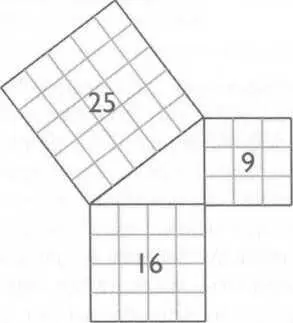
Рис. 74. Точечные узоры появляются в новой форме, чтобы определить стороны треугольника Пифагора

У этого треугольника есть и другая особенность: сумма квадратов двух его коротких сторон (3 и 4) равна квадрату его длинной стороны (5). Это утверждение прекрасно проиллюстрировано на рисунке 74. В мире «настоящей» математики данная квадратичная последовательность записывается так: а 2+ Ь 2= с 2или, в данном случае, З 2+ 4 2= 5 2. Для такого ненавистника математики, как я, менее пугающей выглядит следующая формула: ЗхЗ + 4х4 = 5х5. Удивительно! Эти числа —9, 16 и 25 — вновь отсылают нас к точечным квадратам с рисунка 68, помещенным в начале этой части.

Хотя прямоугольник 3 на 4, с которого мы начали, не таит в себе, подобно магическим квадратам, каких-либо математических сюрпризов, тем не менее, из сложения двенадцати записанных в него чисел образуется сумма 78, что соответствует количеству карт в колоде Таро: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10+11 +12 = 78.

Запомните этот прямоугольник 3 на 4 и, в особенности, треугольник Пифагора, который мы из него получаем. Мы еще встретимся с ним.

Последовательность Фибоначчи — не просто случайная числовая схема, придуманная этим итальянским математиком. Она является плодом осмысления пространственных отношений, имеющих место в природе и впоследствии получившими название золотое сечение.

На Западе числовая последовательность была исследована Леонардо Пизанским, известным как Фибоначчи (ок. 1170-ок. 1240 года н. э.). Происходивший из северной Африки, где его отец заведовал таможней — подсчет был их семейным делом — молодой Фибоначчи в дальнейшем обучался у арабских математиков, затем много путешествовал, всегда обращая внимание на способы записи чисел. Его работа «Liber abaci» («Книга абака», 1202 год н. э., на латыни) ознакомила европейцев с арабскими и индийскими математическими концепциями, включая десятичную систему и индо-арабские формы, которые мы теперь используем для записи чисел [163] Joseph, The Crest of the Peacock, p. 315. . Наряду с латинским переводом «Арифметики» аль-Хорезми, работа Фибоначчи способствовала формированию европейской математической мысли.

В последовательности Фибоначчи каждое новое число является суммой двух предыдущих. Итак, начнем считать с 0, то есть 0+1. Сложив их вместе, вы вновь получите 1, так что корректное начало последовательности будет выглядеть следующим образом: 0, 1, 1.

Новое число — 1 — плюсуется с предыдущим числом — 1 — ив последовательность добавляется число 2: 0, 1, 1, 2.

Сложение финального числа — 2 — с предшествующим — 1 — Дает число 3.

Таким же образом, каждое последнее число добавляется к предыдущему:

0, 1, 1, 2, 3 = 5

0, 1, 1, 2, 3, 5 = 8

0, 1, 1, 2, 3, 5, 8 = 13

Продолжая действовать в том же ключе, вы получите искомую последовательность Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584 и так до бесконечности.

Рис. 75. График Фибоначчи 1,618 Магическое число 1,618… Последовательность Фибоначчи демонстрирует, что при делении каждого числа на предыдущее 1,618… получается вновь и вновь.

Рис. 76. График Фибоначчи 0,618 Магическое число 0,618… Последовательность Фибоначчи демонстрирует, что при делении каждого числа на последующее 0,618… получается вновь и вновь

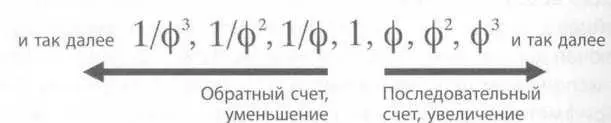
Рис. 77. Счет Фибоначчи

Деление любого числа из последовательности Фибоначчи на непосредственно предшествующее ему дает значение 1,618… (В математическом контексте отточие служит указанием того, что перед нами иррациональное число, то есть имеющее бесконечную десятичную дробь (рис. 75)).

Аналогично, любое число Фибоначчи, разделенное на стоящее непосредственно перед ним, дает примерно 0,618… (рис. 76).

Точность приближения к 0,618… или 1,618… растет по мере возрастания значений используемых чисел. Эти два ключевых числа — 0,618… и 1,618… — являются пропорциональным соотношением между частями золотого сечения — меньшего к большему и наоборот [164] Doczi, The Power of Limits, p. 5. .

Те, у кого в школе было много математики, могут пока передохнуть. Остальным же, для кого знак фи, несомненно, является чем-то греческим, и не более того, объясняю — фи (phi), то есть Ф, используется как одно из обозначений соотношений Фибоначчи/золотого сечения. Раньше мы делили, теперь — будем умножать. Возрастающая последовательность (вправо от единицы, рис. 77) — 1, Ф, Ф 2, Ф 3означает, что.

Греческое обозначение тау

Крест тау

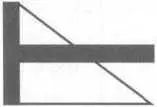
Поперечина тау соответствует короткой «3» стороне (катету) треугольника Пифагора и является «1» в золотом сечении

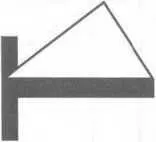
Вертикальная часть тау соответствует длинной «5» стороне (гипотенузе) треугольника Пифагора, играя роль Ф в золотом сечении. Таким образом, соотношение вертикаль-поперечина = = 1,618 (1 х 1,618)

1 — есть начальная точка последовательности Фибоначчи;

стоящая справа Ф — является первым выражением соотношения, то есть, 1 х 1,618..;

ф 2— второе выражение, Ф х 1,618… и т. д.

Сопутствующее символу Ф число указывает на количество сделанных шагов в ряду Фибоначчи, что выражает соотношение между частями лучше, чем конкретные измерения в дюймах или сантиметрах. (При умножении, не включайте отточие.) Соответственно, при обратном счете (влево от единицы, рис. 77) символы обозначаются в виде долей. К примеру, 1/Ф означает 1 х 0,618…