Ренна Шессо - Математика для мистиков. Тайны сакральной геометрии

Все начинается с малого: от кончика пальца к ладони каждая фаланга пальца увеличивается примерно на 1,618 % (рис. 86). При измерении в противоположном направлении следует обратный отсчет (рис. 87).

Продолжим рассмотрение параметров человеческого тела. Так, величина, соответствующая расстоянию от кончика пальца до запястья, взятая 1,618 раза, будет примерно равна длине руки от запястья до локтя. А расстояние от запястья до локтя, взятое 1,618 раза, даст величину, близкую к вашему личному кубиту, с которым мы сталкивались в главе № 3, то есть, расстоянию от локтя до кончика пальца.

Обратившись к своему телу, замерьте длину отрезка от пола (между стоп, без обуви) до пупка и умножьте это число на 1,618. Результат будет весьма схож с расстоянием от кончика до кончика указательных пальцев при распростертых руках, то есть с вашей личной саженью.

Пропорция, лежащая в основе всех этих вещей, известна под разными именами — золотое сечение, золотая середина, золотая пропорция, aureo section (золотое сечение на латыни), сакральное деление, золотое деление, Божественная пропорция. Название немецкого термина — Goldene Schnitt, созвучно золотому снитчу из книг о Гарри Поттере [169] Livio, The Golden Ratio, p. 7. .

Спираль Фибоначчи также может возникнуть из заключенных друг в Друга треугольников (рис. 88). Не важно, под именем тау или фи, золотое сечение является костяком пентакля, повторяясь в различных соотношениях и проявляя свое присутствие на каждом шагу (рис. 89).

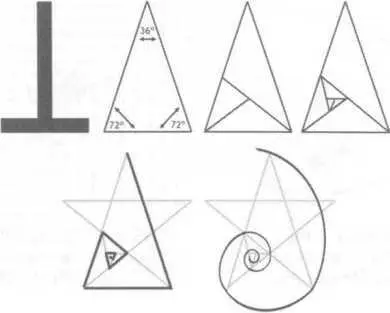
Рис. 88. Спираль Фибоначчи, возникающая в треугольнике на основе may

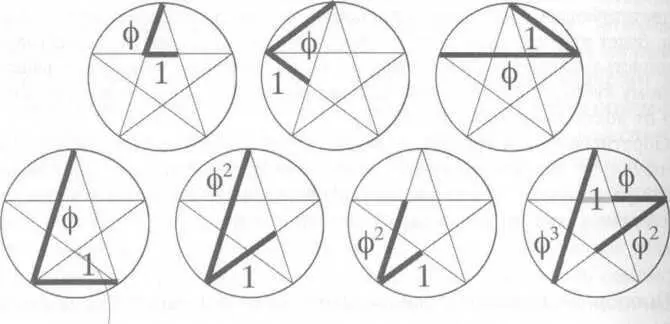
Рис. 89. Пропорции золотого сечения/Фибоначчи, постоянно возникающие в пентакле

Есть простой способ создать пентакль, используя треугольник, изображенный на рисунке 71 в главе № 8. Итак, для его создания потребуется расположить «спиной к спине» десять упомянутых треугольников (рис. 90). Мы можем это сделать, поскольку короткая сторона каждого такого треугольника равна короткой стороне тау («1» в золотом сечении), а длинная — соответствует длинной стороне тау (или фи, Ф, в золотом сечении), как показано на рисунке 78. Кроме того, длины сторон этого треугольника равны 3 и 5 — числам Фибоначчи. Теперь соедините линией каждую пару противоположных углов в пятиугольнике и получите искомую фигуру (рис. 91).

Но, скажем, мы хотим пентакль побольше. Легко, поскольку пятиугольник способен на такие штуки, о чем треугольник или квадрат — двухмерные формы с небольшим количеством сторон — могут только мечтать.

Рис. 90. Построение пятиугольника из десяти треугольников Пифагора

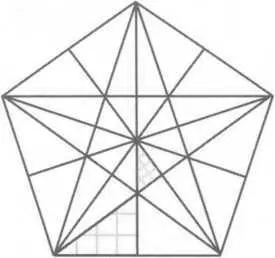
Рис. 97. Добавление линий для создания других треугольников Пифагора внутри пятиугольника

Если продлить линии сторон квадрата или треугольника, то получатся просто линии, устремленные в пространство, которые нигде и никогда не встретятся друг с другом. Но в случае с пятиугольником, линии, продолжающие его стороны, пересекутся и создадут новую форму. Вот так и возникнет наш пентакль (рис. 92). Соединение углов этой новой звезды прямыми линиями образует новый пятиугольник. Окружите концы звезды кругом, и вы получите настоящий магический знак, олицетворяющий всю скрытую в нем гармонию формы и взаимосвязи; сочетание круга и креста тоу образует скипетр Императора, символизирующий объединение и преобразование.

Примерно в 2400 году до н. э. вавилоняне определили круг как величину в 360°, основываясь на грубом подсчете количества дней в году. Триста шестьдесят является необычайно полезным и многосторонним числом, о чем знали вавилоняне — специалисты по наблюдению за небом. Математический потенциал его широк, поскольку 360 может быть разделено без остатка на любое из следующих двадцати двух чисел: 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 и 180 [170] Pickover, Passion, p. 270. . (Хм… двадцать два… это количество карт Старших Арканов в колоде Таро).

Разделение круга на градусы позволяет нам отмечать долготу и широту и астрологически очерчивать пространство. В комбинации с нашим пентаклем круг также обладает любопытным набором математических особенностей. Разделите 360 градусов круга на 5 (пять концов пентакля) и вы получите пять сегментов по 72° каждый (рис. 93). Зафиксированные на окружности, эти точки соответствуют углам в 0°, 72°, 144°, 216°, 288° и вновь 0°, составляя, таким образом, 360°. Упростим эти числа, как мы уже делали в этой книге. Вы увидите, что все они сведутся к 9.

Если мы слегка повернем нашу звезду, как бы для создания десятиконечной — путем наложения другой 5-конечной звезды поверх первой — концы новой звезды будут располагаться в точках 36°, 108°, 180°, 252° и 324°. И вновь, каждое из этих чисел упрощается до 9.

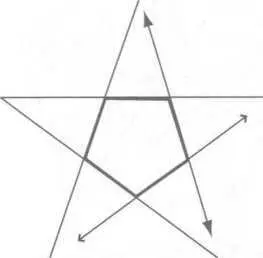
Рис. 92. Продлив линии сторон любого простого пятиугольника, вы создадите пентакль

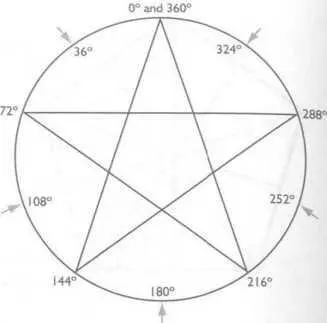
Рис. 93. Внутри 360° круга градусное значение всех точек, на которые попадают вершины пентакля, упрощается до 9. Начните с другого начального градусного значения, и вы получите другой результат

Конечно, мы будем совершенно неправы, если скажем, что это единственные числа в пределах 360°, которые упрощаются до 9. Напротив, таких чисел много. Возьмите любое, например, само число 9. Концы звезды отстоят друг от друга на 72°, поэтому добавив 72° к новой стартовой точке — 9, 81, 153, 225 и 275 — вы получите другой пентакль или пятиугольник, градусные значения всех вершин которого упрощаются до 9.

Но любые ли пять точек, отстоящие друг от друга на 72°, всегда дают пентакль с подобными свойствами? Вот и нет! В случае избрания другого стартового градуса каждый угол в этом пентакле будет упрощаться до его значения:

1°, 73°, 145°, 217° и 289° все упрощаются до 1 (часто через 10 или 19);

13°, 85°, 157°, 229° и 301 ° (все упрощаются до 4 (через 13)).

Это верно даже в случае с дробями: просто обращайтесь с ними, в процессе упрощения, как с отдельными разрядами, не обращая внимания на разделительную запятую: