Рубен Ишханян - Тюрьма для свободы

В кабинете геометрии висели репродукции картин. На них были изображены все известные ученые, начиная от Евклида и Пифагора, заканчивая Дэвидом Мамфордом и Даниэлем Квилленом. Ее уроки не были сухим изложением знаний. Она старалась сделать все возможное, чтобы ученики погрузились в мир геометрии. Знала, в любом случае, каждый умный человек в своей жизни будет задаваться вопросами о пространстве и времени.

«Дети, — говорила она, — умные люди до сих пор головы ломают, желая понять то, что я вам объясняю. Слушайте меня. Вполне возможно, вы станете намного умнее взрослых. Большинство, плохо проучившись в школе, желают восполнить пробелы в своих знаниях. Они не учитывают, что для каждой информации есть свое время».

На ее уроках Эрл всегда сидел за партой перед учительским столом. Это заставляло его скрывать усталость. Он слушал учительницу так напряженно, как это было возможно. «Геометрия — наисложнейший предмет», — говорил он раздраженно, когда не справлялся с задачей. Однако это бывало очень редко. Чаще всего он увлеченно старался осилить. Закончив, хвастался. Ощущал прилив позитивных эмоций. Начинал громко смеяться и ликовать.

«Как известно, древнегреческий математик Евклид мировую известность получил благодаря своему труду под названием „Начало“. Там изложены все факты геометрии и теоретической арифметики», — начала урок учительница. Эрл смотрел на нее и думал о том, откуда у взрослых столько энергии. Меж тем учительница продолжала. — «Евклид, как и Аристотель, был учеником Платона. Последний большое влияние оказал на их становление. Платон уделял внимание бытию и небытию. Согласно его мировоззрению небытие можно понимать двояко. С одной стороны оно является зеркальным отражением бытия, с другой стороны небытие это нечто иное по отношению к бытию. В скором же времени в своем труде „Софист“ он отрекся от мысли, что небытие как противоположность бытию должно быть исключено. И тут кроме вопроса „Что это есть?“ Платон поднимает немаловажный вопрос: „Почему?“. В дальнейшем платоновское „Почему?“ станет для Аристотеля теоретическим вопросом. Ответить на этот вопрос означает найти причину и обоснование. Вспомните картину Рафаэля Санти „Платон и Аристотель“. В образе Платона изображен Леонардо да Винчи. Можно увидеть, что Платон держит книгу „Тимей“, а Аристотель свою „Этику“. В трактате „Тимей“ Сократ, Тимей, Критий и Гермократ входят друг с другом в диалог. Не случайно представлены четыре философа. Каждый из них олицетворяет один из четырех правильных многогранников: тетраэдр — огонь, октаэдр — воздух, икосаэдр — вода, куб — земля».

Учительница подошла к доске. Взяла в руки мел и посмотрела на класс.

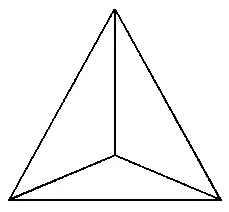
«Правильными считаются те многогранники, которые выпуклы, все грани равны и в каждой его вершине сходится одинаковое число рёбер. Они характерны для философии Платона. Тетраэдр — четырехгранник, все грани которого — треугольники».

И она нарисовала следующее:

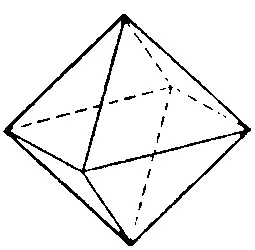
«Октаэдр — тело, ограниченное восемью треугольниками».

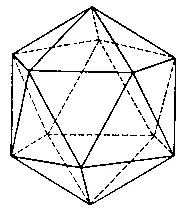
«Икосаэдр — тело, ограниченное двадцатью многоугольниками».

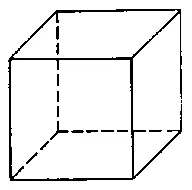
«Куб — правильная четырехугольная призма с равными ребрами, ограниченная шестью квадратами».

«Но существует еще и пятый многогранник — додекаэдр, который „достался в удел фигуре вселенной“».

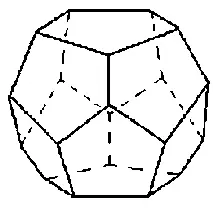
«Считается, что трактат „Начало“ Евклида можно рассматривать как развернутое учение о построении пяти правильных многогранников. На самом деле это так. Вся XIII книга „Начала“ посвящена изучению правильных многогранников. В этой части Евклид предпринимает попытку построить все пять правильных многогранников и вписать их в шар. Старается найти отношения между стороной каждого правильного многогранника и диаметром шара. После этого он сравнивает стороны правильных многогранников, вписанных в один и тот же шар. И его попытка сделать многогранники равновеликими сталкивается с трудностями.

Евклидова геометрия имеет и иное название. Ее часто считают элементарной геометрией, которая изучается в средней общеобразовательной школе. Евклид дает в своем труде основные арифметические определения:

точка есть то, в чем нет никакой части;

линия — длина без ширины;

края линии — точки;

поверхность есть то, что имеет только длину и ширину;

края поверхности — линии;

тело есть то, что имеет длину, ширину и глубину;

край тела — поверхность.

И в этих определениях нет ничего странного с современной точки зрения. Однако необходимо помнить, что математика зародилась в VI веке до н. э., а Евклид жил в III веке до н. э. Вот, какую цепочку следует выстроить:

нульмерный объект — точка;

одномерный бесконечный объект — линия;

одномерный конечный объект — отрезок;

двухмерные объекты — плоские;

трехмерный бесконечный объект — пространство Вселенной (если бы она была евклидова и статична);

трехмерные конечные объекты — куб, шар, пространство комнаты и так далее;

четырехмерный объект — пространство-время».

Учительница говорила о четырехмерном объекте, который представляет собой пространство и время. Но она не говорила, что евклидово пространство и есть четырехмерное пространство.

Тогда Эрл не знал о существовании пространства Минковского. Но в тюрьме, в этом пустом пространстве его мысли сами привели к этому. Он открывал для себя то новое, что до него уже было изобретено. За неимением знаний, заключенный стал вести дневниковые записи. Писал на листе бумаги мысли, возникающие в потоке сознания. Тогда заметил, что абсолютно все знания на генетическом уровне уже живут в нем. На каждый возникающий вопрос, мгновенно находился ответ. Еще со школьных лет он знал о трехмерном пространстве. Всегда считал, что это не самое правильное решение. Пространство не может существовать без времени. Пространство и время не абсолютные понятия. Он осуждал евклидово пространство. Находил в нем изъяны. По сути, теория Евклида представляет собой n -мерное векторное пространство. В него возможно ввести некоторые специальные координаты (декартовы пространственные координаты — x 1,x 2,x 3).