Альманах - Альманах «Российский колокол» №2 2021

Титульный лист первого издания труда И. Кеплера «Гармония мира». Франкфурт, 1619 г.

Великий ученый XVIII в. Леонард Эйлер (1707–1783 гг.), член Петербургской академии наук, среди более 850 своих научных трудов ряд работ посвятил музыке. Одна из первых больших работ Л. Эйлера – «Dissertatio physico de sono» – посвящена природе, образованию и распространению звука. В 1726 г. Л. Эйлер писал Даниилу Бернулли [2] Бернулли Даниил (1700–1782). , что для ноты «до» он в результате исследования получил 139 колебаний в секунду. В 1727 г. Л. Эйлер, находясь в Петербурге, составляет отчет о своей работе в виде «исчисления всех дел, елико ко умножению и совершенству наук принадлежат, доселе произвели и что впредь произвести намерены…

Л. Эйлер, профессор высшей математики адъюнкт, уже исследованию предложил:

1. Физико-математическое рассуждение о звуке или звоне, в котором новая звону теория предается и поставляется, откуда производится образ счисления (вычисления. – В. С.) скорости звука;

2. Рассуждение о качательном (колебательном. – В. С.) движении струн, колоколов, барабанов, которые через

ударение звон издают, где от теории каждого инструмента изъявляется образ счисления скорости звука;

3. О произведении звона или звука пушечного, громового и прочих таковых.

4. Новая теория о звонах или голосах флейт, труб и других инструментов, которые через надувание глас издают».

Основным трудом Л. Эйлера по вопросам теории музыки стала «Tentamen novae theoriae musicae, ex certissimis harmoniae principiis dilucide expositae» [3] На русском языке название книги Л. Эйлера выглядит так: «Опыт новой теории музыки, ясно изложенный на основе несомненных принципов гармонии». Перевод книги в 1959 г. автору статьи помогала осуществлять преподаватель ОГУ Н. Л. Сикорская, которой автор остается благодарен и поныне. Методическую помощь при написании студенческой работы, за которую автор получил премию, оказывали преподаватель школы Столярского В. А. Швец и доцент кафедры математического анализа университета С. Н. Киро, которым автор также выражал благодарность, но напечатать в студенческой работе это не разрешили. Поэтому уместно эту благодарность выразить в данное время, через 50 лет после написания работы. , напечатанная в 1739 г. в Санкт-Петербурге и найденная автором в научной библиотеке Одесского госуниверситета. Музыку Л. Эйлер воспринимал как гармонию пропорций. Возможно, такие представления были заимствованы у И. Кеплера из его капитального труда «Welt-Harmonik» («Гармония мира»), изданного в 1619 г. во Франкфурте и переизданного в Мюнхене – Берлине в 1939 г. («Земля и Вселенная», 2002, № 5).

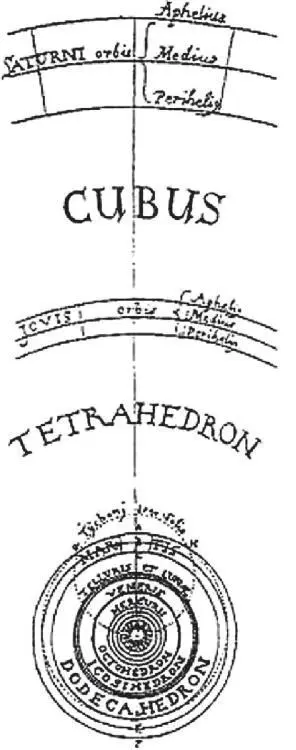
План планетных орбит, построенных с помощью вписанных и описанных многогранников, показанный в книге И. Кеплера «Гармония мира». Расстояния до планетных орбит автор определяет в соответствии с построением золотого сечения, используя длину энергетической стоячей волны

Как писал в своем труде Л. Эйлер, его теория музыки строится на двух основаниях: физическом (физические законы звука) и метафизическом (изучение восприятия звука). Л. Эйлер рассматривает вопрос: что есть общего между консонансами и отношениями целых чисел, соответствующих, согласно современной терминологии, частотам колебаний струн, образующих созвук при одновременном звучании, вызванном этими струнами? Ответ на подобный вопрос частично дали, И. Кеплер и даже древний философ Пифагор.

Со времен Пифагора известна легенда о том, что Пифагор, проходя мимо кузницы, услышал звуки, которые издавали два молота, стучавшие по наковальне. Получилось соотношение музыкальных тонов, дававших определенный музыкальный интервал. Пифагор сравнил молоты и нашел, что по их форме и размерам можно было найти такое же отношение (пропорцию) при звучании, вызванном колебаниями струн. Оказалось, что чистая кварта дает отношение 4:3, квинта – 3:2, секста -5:3, большая терция – 5:4, малая терция – 6:5. Следовательно, отношение простых чисел дает восприятие консонанса, а секунда (16:15) воспринимается как диссонанс. Л. Эйлер пишет: «Если мы при восприятии звуков не улавливаем никакого порядка или этот порядок неожиданно нарушается, мы не можем почувствовать удовлетворения». Иначе говоря, слушателю приятно все то, в чем он улавливает завершенность, определенный порядок. Такой порядок создается при наличии определенного правила, из которого можно сделать заключение, почему часть целого помещена в том или ином месте. Такое рассуждение напоминает о понятии, создающем образ гармонии при делении отрезка в средне-пропорциональном отношении, когда, в частности, целое так относится к большей своей части, как большая часть – к меньшей:

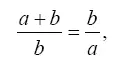
при а = 1, b = х, х 2– х – 1 = 0.

Так эта пропорция превращается в уравнение с корнями ± Ф, обладающими рядом удивительных свойств. Например, если число n = 0, 1, 2, 3…∞, то корни приведенного уравнения могут составить следующую зависимость Фn + Фn+1 = Фn+2, которая определяет единство аддитивных и мультипликативных свойств этих чисел, образующих ряды Фибоначчи, благоприятно осуществляемые при развитии всевозможных природных явлений (например, размножение кроликов) [4] В математике аддитивность означает, что каждый предыдущий член ряда чисел Ф 1 , Ф 2 , Ф 3 … равен сумме двух последующих: Ф 1 = Ф 2 + Ф 3 и т. д. Мультипликативность означает, что в том же числовом ряду все члены связаны геометрической прогрессией: Ф 1 :Ф 2 = Ф 2 :Ф 3 . . О записанной выше «божественной пропорции», или «божественном» (золотом) сечении, уже сказал И. Кеплер при рассмотрении геометрии снежинок.

Как выяснилось в дальнейшем, осуществление золотого сечения в природе определяет в огромном числе случаев не только музыкальное восприятие, но и само развитие этой природной формы в наиболее благоприятном направлении, например развитие листьев или рост кроны дерева. В книге «О шестиугольных снежинках» (в переводе с латинского эта книга выпущена на русском языке издательством «Наука» в Москве в 1982 г. по изданию 1611 г. во Франкфурте-на-Майне) Кеплер писал: «По образцу и подобию продолжающей саму себя пропорции сотворяется, как я полагаю, производительная сила, и этой производительной силой запечатлен в цветке смысл пятиугольника».

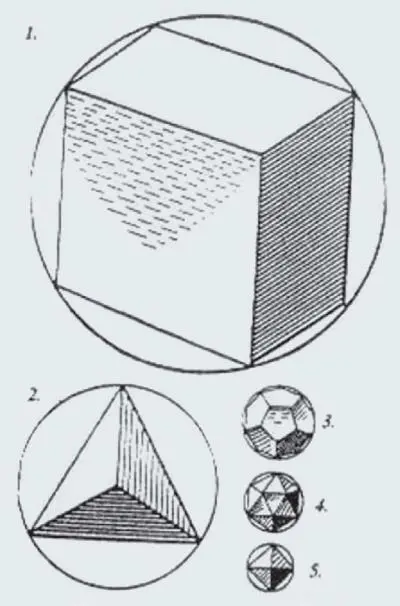
Космические комбинации платоновых фигур, позволяющие, согласно И. Кеплеру, построить планетные орбиты в Солнечной системе: 1 – куб, 2 – тетраэдр, 3 – додекаэдр, 4 – икосаэдр, 5 – октаэдр