Марина Мыльникова - Активация системы каналов акупунктуры человека

© Марина Сергеевна Мыльникова, 2018

ISBN 978-5-4493-8508-6

Создано в интеллектуальной издательской системе Ridero

Что подразумевается под термином материализация? Математическая единица и материальная точка абстрактны. Без математики они отсутствовали как понятие, но без них теоретические труды не обошлись бы, не было математического обобщения, теоретической базы для практической индустрии. Из небытия извлеченные в информационный пласт эфемерные понятия явились краеугольными камнями множества практических вычислений.

Рис 1 —

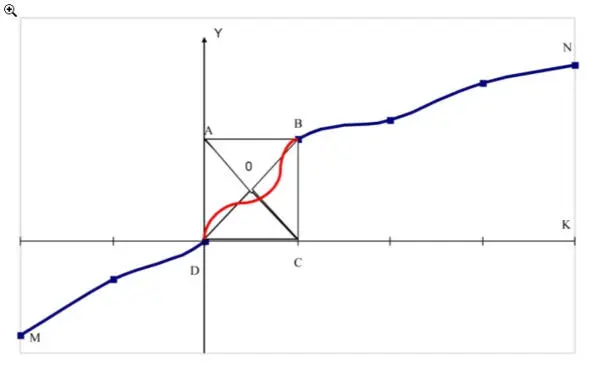
Рассмотрим процесс Mn (кривая) и случай В этого процесса (точка В).

Обнаруживается, что правильно описать этот процесс невозможно, т.к. само описание не имеет конца, и вероятно только описание заданных, т.е. известных характеристик.

Получив две координаты, точка становится «квадратной», со сторонами х и у. Если добавить ось Z, задающую объем, точка становится кубом со сторонами х у z, если х = у = z и параллелепипедом, если х ≠ у ≠ z. При появлении дискретной вращательной характеристики точка будет стремиться к форме многогранника, а постоянная вращательная характеристика превратит ее в шар, т.е. точка примет изначально предполагаемую форму, «круглую».

Первоначальное описание двумя координатами можно рассмотреть в качестве случая материализации точек А и С, которых «не было» и которые «возникли» при необходимости описать точку В.

Относительно друг друга они равны нулю, относительно точки В имеют числовую характеристику. Запомним этот факт. В квантовой физике так «ведут себя» противоположные спины.

Назовем ∆АСД координатной сферой описываемой точки В; ∆АВС отражением координатной сферы.

Рассмотрим материализацию (здесь и далее термин материализация употребляем как банальный) на данном примере. ∆АВС ограничен вспомогательными перпендикулярами на оси координат и гипотенузой АС, которая служит границей между координатной сферой и ее отражением.

∆АДС имеет значение для системы координат х у с центром в точке Д и для процесса описания он сам является описанием «разреженной» точки В, в сущности, это материализованное квазипространство, то есть мы получаем пример возникновения и, далее, узаконивания, этого понятия, и, более того, прямого участия в движении твердого материального мира таких объектов, как материальная точка и математическая единица. Этот процесс автор и называет материализацией, а вышеописанное есть случай материализации.

Однако, и точка, и единица являются квазивеличинами, т.к. они находятся в квазипространстве.

Здесь уместно привести описание существования абсолютного параллелизма для напоминания о геометрии Римана.

«В одной точке Ро ориентацию локального ортогонального n-кода можно выбрать произвольно. Но для других точек она уже будет определяться однозначно условием, чтобы все соответственные оси локальных n-кодов были взаимно параллельными. Тогда параллельные векторы будут иметь одинаковые локальные компоненты. Таким образом, для параллельного переноса вектора А из точки Ро в безконечно (православная орфография приставки «без» здесь и далее) близкую точку Р 1выполняется формула

,

или, т.к. компоненты линейного элемента dx υ= αh υαdх,

а обратные соотношения имеют вид

αdx = αh υdx δυ,

то

Полагая, что

перепишем закон параллельного переноса в виде:

.

Здесь величины ∆ в известном смысле аналогичны символам Кристоффеля rστ νв геометрии Римана, поскольку они являются коэффициентами в соотношении, выражающем закон параллельного переноса. Однако, именно в этих величинах проявляется противоположность двух структур. Величины Г в геометрии Римана симметричны по нижним индексам, но выраженный через них закон переноса не интегрируется.

Величины ∆, напротив, не симметричны, но выражаемый через них закон переноса интегрируется.

Величины ∆, как и образованные из них антисимметричные выражения

Λ στ υ= Δ υ στ – Δ υ τσ

обладают тензорным характером.

Свертыванием этого тензора получается вектор

φ σ=Λ ά σά

играющий в физических приложениях теории роль электромагнитного потенциала.

Существование тензора обуславливает наличие инвариантов и их первых производных. C функцией Гамильтона запишем вариационный принцип для таких вариаций величин hυ, которые обращаются в нуль на пределах интегрирования. Тогда получаются 16 уравнений для 16 полевых переменных h.

Разработка и физическая интерпретация затруднялась по той причине, что для выбора соотношений между постоянными А, В и с априори не было известно никаких оснований, т.к. при выборе постоянных

В = -А,

С = 0,

получаются уравнения поля, в первом приближении согласующиеся с известными законами гравитационного и электромагнитного полей.

Вычисления, проведенные совместно с Г. Мюнцем, показали даже (отметим этот момент знаком»!»), что поле материальной точки без электрического заряда в развитой здесь теории в точности совпадает с полем, которое дает первоначальная общая теория относительности.

Прежде чем вернуться к рассмотрению процесса материализации единиц, скажем, что вектор, играющий в физических приложениях теории роль электромагнитного потенциала, вследствие антисимметричности относится к интегрируемым величинам, т.е. такое описание позволяет рассматривать электромагнитный потенциал не как волну, а как частицу.

В геометрии Римана тот же закон пространственного переноса ведет к рассмотрению аналогичных величин как симметричных и неинтегрируемых, т.е. волн.

Сделаем вывод, если можно так выразиться:

Перпендикулярная система отсчета позволяет реализовать перпендикулярные и (или) скрещивающиеся свойства исследуемой единицы, т.е.при В = -А, С = 0 в перпендикулярной системе отсчета В + С ≠ В, -А – С = -А-1.

Можно сделать и другие всевозможные выводы, простейший повторный анализ рис.1. проиллюстрирует это.

Вспомним, что, получив две координаты, точка стремится к квадрату, 3-к кубу, множество – шару. Если учесть, что все процессы происходят во времени, ко всему – и к точке, и к процессу, и к системе, и к описанию процесса, т.е. к производной – добавляется векторность, являющаяся по отношению к прочим характеристикам квазисвойствам, т.е. векторность в своем роде четвертый лишний.

Сама точка В материальна, принадлежит кривой МN, т.е. является случаем процесса МN, точка В является целым, это дифференциал из интегрированной системы МN.