Михаил Бармин - Теоретическая механика. Часть 4. Динамика системы материальных точек и твердого тела с решениями задач

(1.2)

Допустим, М.С. является твердым телом, находящимся в равновесии ( и одинаковы). Тогда, согласно теореме об изменении кинетической энергии, имеем, дав телу элементарно малое возможное перемещение “” какой—либо внешней силой “”

, но и

Если тело поместить на плоскость с трением (), то при перемещении тела по этой плоскости

Объединив эти соображения, имеем (1.3)

В выражении 1.3. принципа возможных перемещений (П.В.П.) S=1S—число степеней свободы системы, равное числу возможных (виртуальных) её перемещений, допускаемых наложенными на М.C. связями.

Пример на П.В.П.:Балка АВ находится в равновесии под действием сил и . Плечи сил”а” и “ b” известны. Каково должно быть соотношение сили , т. е. Р = F(Q)=? (Рис. 1.3).

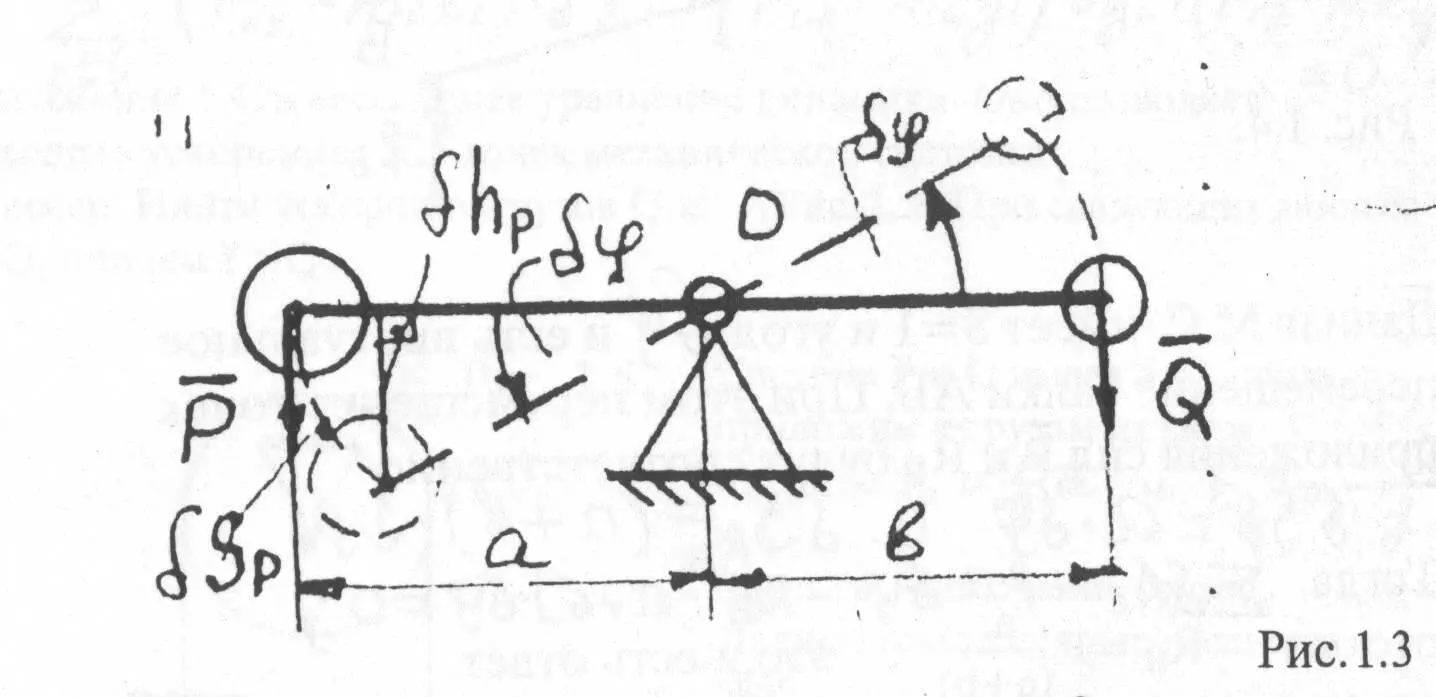
Система имеет S=1, описываемое углом “” поворота вокруг оси “O”. Считая, ввиду их малости ““= и ,

Определим

Отсюда . Это ответ.

Применим П.В.П. К задачам статики. Там тело изначально находится в равновесии, т.е. заведомо.

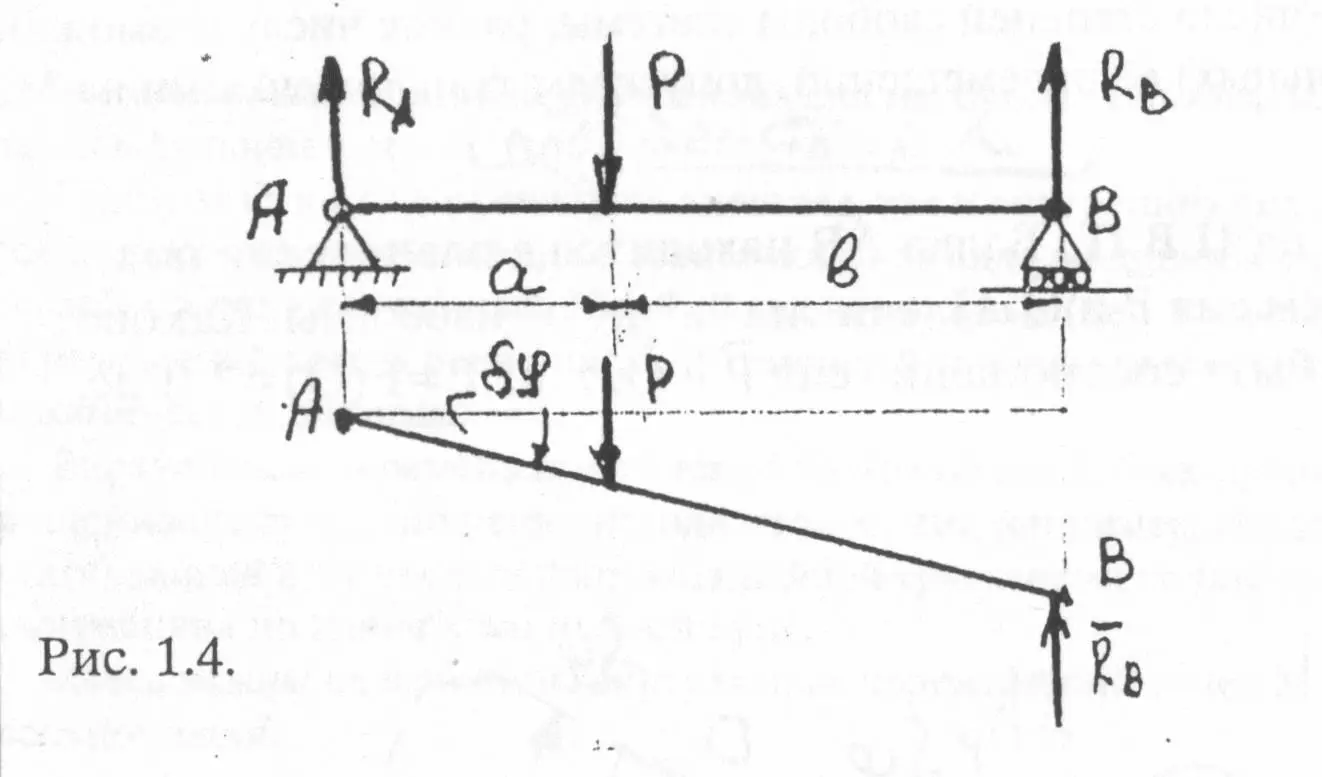
Пример:

Определить реакцию балки АБ при следующих

данных: Р, а,

b

. (Рис.1.4.

)

Данная М.С. имеет S=1 и угол и есть виртуальное перемещение балки АВ. При этом перемещение точек приложения сил и будут соответственно

и . Тогда отсюда ; это и ответ.

Р.S.: Решая задачу методами статики, имеем: т.е..

Так что задачи статики можно решать и П.В.П.

1.3. Принцип Даламбера и общее уравнение динамики механической системы и твердого тела.

Формулировка принципа Даламбера:

Если к каждой точке механической системы с двухсторонними связями помимо сил, на них действующих, приложить еще и силу инерции (), то все силы, действующие на все точки М.С. будут взаимно уравновешенны и к такой, уже уравновешенной системе сил, можно применить все законы статики,а также и П.В.П.

При этом .

Спроектировав на оси декартовой системы координат выражение 1.4, имеем:

(1.4).

Выражение 1.4. и есть общее уравнение динамики. Оно позволяет

находить ускорения “” точек механической системы.

Пример: Найти ускорение грузов Q и (Рис. 1.5) При следующих данных:

P, Q, причем

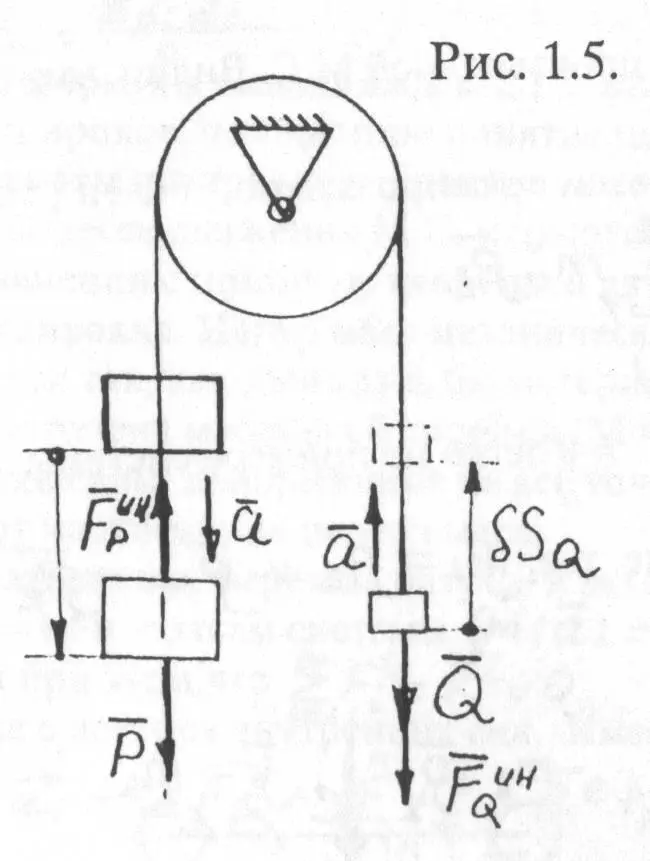
Система Р и

Q

имеет

S

=1, тог

l

а приложим к грузам их силы

инерции и

Здесь “a”– ускорение грузов. Дадим возможное перемещение

Тогда:

Отсюда имеем: Это ответ.

Рис 1.5

Известно, что . При Q=P имеем a=0 – равновесие системы.

ЛЕКЦИЯ №2

1.4. Центр масс механической системы и твердого тела и теорема о его движении.

Центр масс механической системы любого числа “n” материальных точек в произвольном его движении это точка (или место в пространстве внутри системы), для которой выполняется следующее векторное равенство: (1.5)

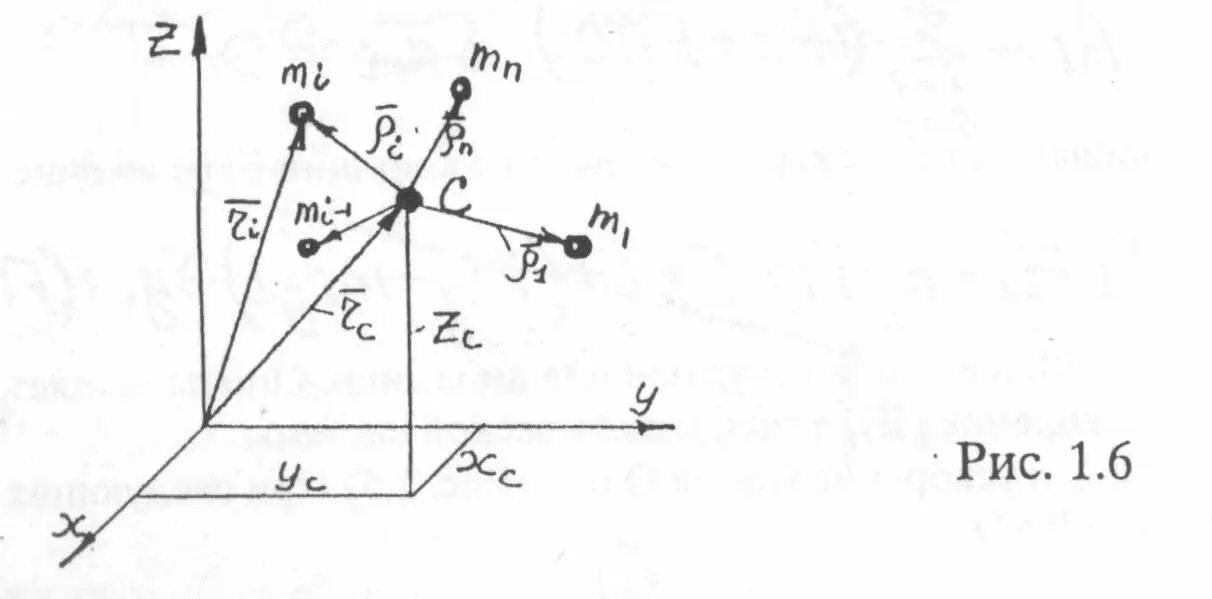
На рис. 1.6. изображен центр масс “C” произвольной М.С. Видно, что . Если произвести умножение на , а затем суммировать по “i=1n”, то имеем:

. Отсюда . (1.6)

Понять, почему для () С легко на примере системы 2х точек .

(Рис. 1.7), для которой () С будет посредине, т. е. и

Здесь векторная сумма

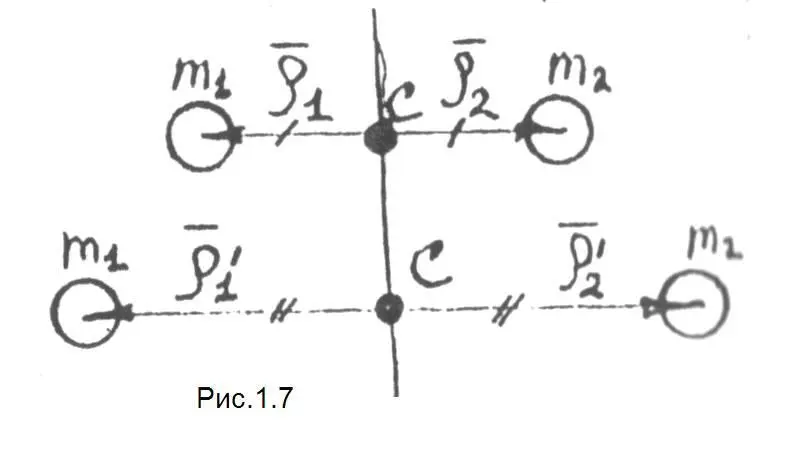
Если данная система симметрично разойдется, при этом центр масс “С” останется на месте. В этом несовершенство данного понятия, т.к. () С не отражает некоторых возможных (виртуальных) перемещений, опускаемых связями, наложенными на систему.

Спроектирован 1.6. на оси декартовой системы координат (Рис. 1.6) и учтя, что массе всей системы, имеем:

,, (1.7)

Это формулы определения координат центра масс “С”.

Если для вех точек “” системы ускорение свободного падения 9,81 м/, то умножая и деля на g выражения 1.7 получим координаты центра тяжести твердого тела весом Р=Mg, т.е.

; ; . (1.8)

Эти формулы выводились в ч. 1 – статике. В целом понятие центра масс более широкое, чем частное понятие центра тяжести. В ряде случаев координаты центра масс и центра тяжести не совпадают по положению.

В процессе движения М.С. меняются координаты () С. Установим закон их изменения с помощью теоремы о движении центра масс. Формулировка.Центр масс механической системы (и твердого тела) движется так, как двигалась бы материальная точка, в которой сосредоточена масса всей системы (М=) и к которой приложены все – внешние силы, действующие на все точки системы. Внутренние силы () не влияют на движение центра масс.

Доказательство. Берем за базу 2—закон Ньютона применяем его ко всем i=1/n точкам системы (). Учтем при этом, что ,

т.к. это свойство главного вектора внутренних сил. Имеем:

. Выясним, чему равна , учтя, что и по рис.1.6.

Имеем: , т.е. Тогда 1.9

Это и есть закон движения центра масс механической системы и Твердого тела. Видно, что только внешние силы влияют на его движение.

Часто М.С. получает движение как раз из—за наличия в ней внутренних сил , но эти внутренние силы вызывают внешние реактивные силы которые и влияют на движение центра масс “С”.

Это легко понять, анализируя процесс выстрела снарядом из ствола орудия. Система ствол—снаряд за счет внутренних сил давления пороховых газов получает движение вида: снаряд—направо, орудийный ствол– налево. Так возникает “отдача” при выстреле. Орудие контактирует с внешней средой и при откате его возникает реакция внешней связи которая входит в группу всех внешних сил, так что выражение 1.9. Можно

расширенно записать так:

1.10

В выражениях 1.10 имеем дифференциальные уравнения движения () С, интегрируя которые можно получить кинематические уравнения движения () С, т.е. x=x(t), y=y(t) и z=z(t).

1.5. Понятие о моментах инерции”I” механической системы и твердого тела. Более объемной характеристикой распределения масс “m” внутри механической системы и твердого тела любой формы является понятие о

моментах инерции”I”.

Если условие существования центра масс ( ) не всегда отражает истинное положение точек “mi” системы (Рис. 1.7), то для “I” имеем: Здесь поэтому и чем больше ,тем больше I.

Различают плоскостные, осевые и полярные моменты инерции. Определим их для твердого тела в системе декартовых осей (рис.1.8).

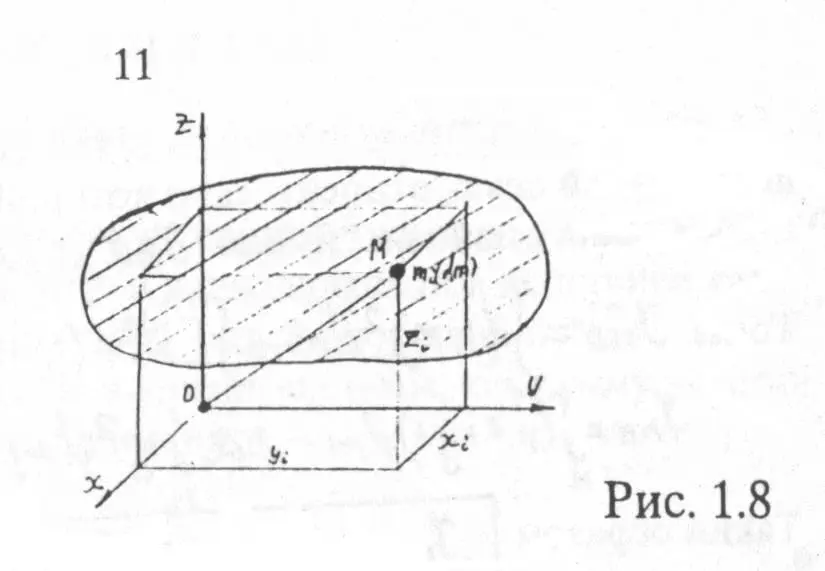
Плоскостные J: ;