Михаил Бармин - Теоретическая механика. Часть 4. Динамика системы материальных точек и твердого тела с решениями задач

М.И. Бармин

Динамика системы материальных точек и твердого тела (часть IV) с решениями задач

Конспект лекций ориентирован на объем курса до 102 часов для студентов

технологов различных специальностей.

Краткий конспект лекций по теоретической механике с включением примеров решения типовых задач по всем темам курса.

Составлен на базе анализа лекций курсов теоретической механике для ряда технологических вузов различных направлений. Является основой для освоения студентами инженерных дисциплин, таких как “Сопротивление материалов”, “Теория механизмов и машин”, “Детали машин”, “Подъемно – транспортные устройства и др. ”

Михаил Иванович Бармин родился в городе Ленинграде 15 января 1948 года. Окончил Ленинградский технологический институт (Технический университет) в 1973 году. Инженер химик-технолог (химия и технология высокомолекулярных соединений). Более 8 лет производственного опыта (органический синтез на полупромышленных установках по синтезу новых органических соединений). Закончил аспирантуру в срок в 1985 году. Кандидат химических наук (химия и технология гетероциклических соединений).Удостоин звания доцента в 1985 году.

Действительный член Нью-Йоркской академии наук (1995-1998 гг.), Соросовский доцент (2001, 2002), лауреат премии «Грант Санкт-Петербурга» (2002). С 1972 года занимается научной деятельностью. Автор более 180 научных и методических трудов (в том числе 3 монографий, 2 обзора , 22 изобретения), автор и соавтор 5-и технологий.

Автор сайта http://www.teachmi.ru/– обучение химии на всем протяжении этого процесса от школы до аспирантуры. На сайте будут предложены авторские лекции и книги по химии, впоследствии по всем предметам 1,2 курса университета. Можно приобрести некоторые реактивы, купить лицензии на новые технологии в области химии. В настоящее время работает на кафедре теоретической и прикладной химии Санкт-Петербургского государственного университета технологии и дизайна в должности доцента.

Динамика системы материальных точек и твердого тела

ЛЕКЦИЯ 1

Понятие системы материальных точек; связи, налагаемые на систему (внешние и внутренние); степени свободы “S” различных механических систем.

Система материальных точек – это совокупность любого их числа (i=1:n, причем n), рассматриваемая в совместном движении.

Примером может служить любая звездная система, например, солнечная. Материальные точки (М.Т.) , т. е. точки, масса “m” которых известна, включаемые в механическую систему (М.С.) могут быть связаны между собою различными связями внутри М.С. Такие связи называют внутренними связями.

В случае, когда М.С. имеет только внутренние связи, ее движение в пространстве ничем не ограничено и такая система называется свободной. В части II – кинематике рассматривается вопрос о числе степеней свободы свободной неизменяемой системы с (“i =1-n”) неограниченным числом “n” материальных точек. Там, базируясь на выражении S=3n-K, где “К” – число внутренних связей, мы приходили к выводу, что свободное абсолютно твердое тело (Т.Т.) имеет S = 6 степеней свободы и для описания его механического перемещения в пространстве нужно соответственно б кинематических уравнений движения. Задачей динамики твердого тела будет вывести эти уравнения, базируясь на дифференциальных уравнениях движения и интегрируя их. Связи, налагаемые на М.С. могут быть как стационарными (неизменяемыми), так и односторонними. Например (Рис. 1.1.) в случае “А” точки системы связаны жестким невесомым стержнем постоянной длины “I”= const. В случае “В” они вязаны пружиной, которая может менять свою длину “I” под действием внешних сил “Fe”, действующих на систему, и эта система геометрическиизменяемая, а связь неудерживающая.

Односторонние связи (нить, например) препятствуют движению М.Т. в одном каком—то направлении (Рис. 1.1, В)

Различают связи геометрические (голономные), которые ограничивают движение М.Т. системы в пространстве, не влияя на их скорость “

V

i” и

дифференциальны

е(неголономные), которые, помимо ограничений в перемещении точек М.С., влияют еще и на их скорость.

Так, например, гладкая поверхность (без трения) является для тела геометрической связью, а шероховатая (с трением) – дифференциальной (Р.

S

. – в ч.

I

, статике, эти связи назывались соответственно идеальными и связями с трением).

Связи, наложенные на М.С. могут быть внешними, действующими извне на М.С.и внутренними, связывающими М.Т. внутри системы (Рис. 1.2.А)

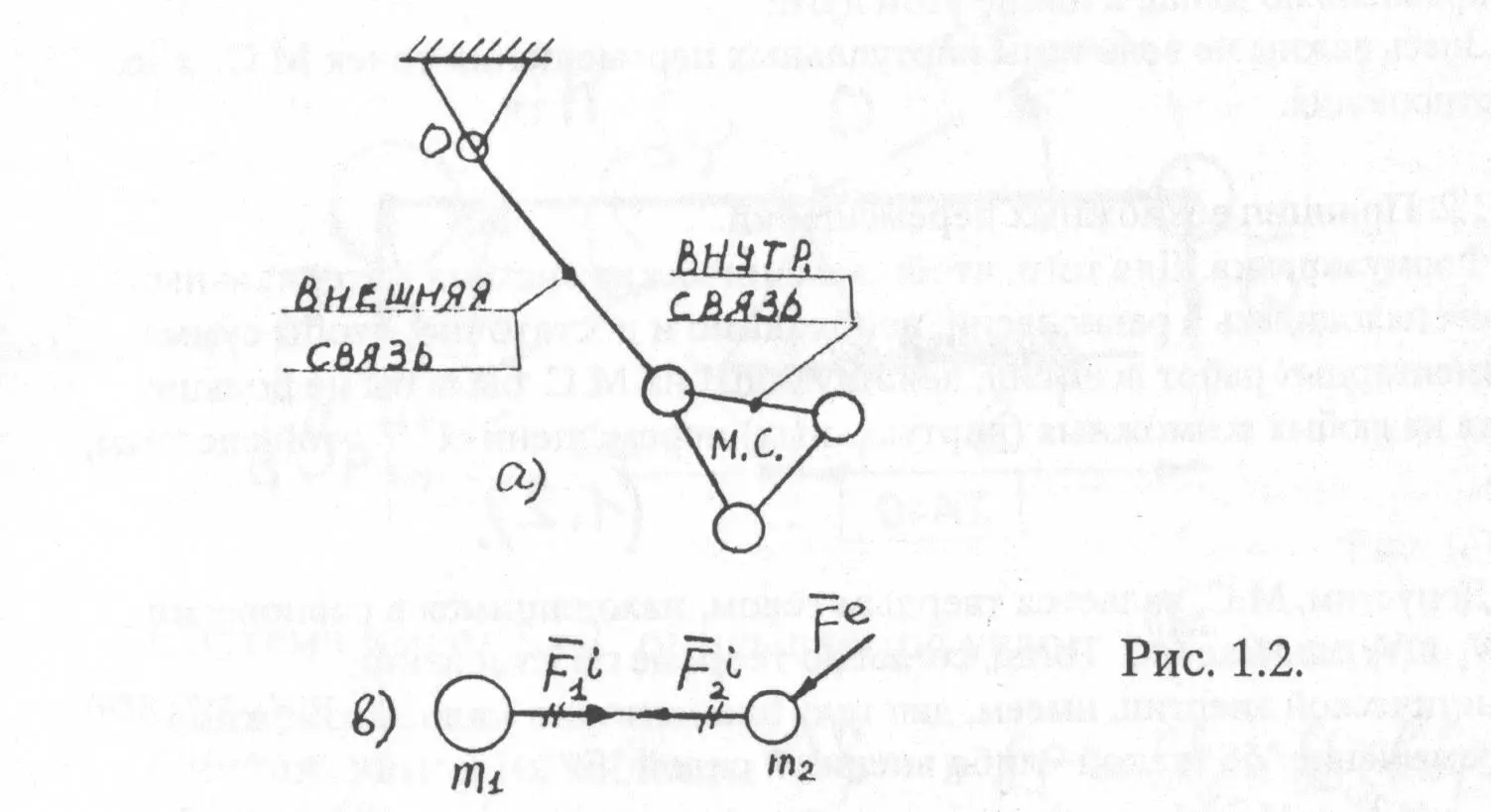
Если на систему наложены внешние связи, то она считается несвободнойи число ее степеней свободы S<6.

Силы, действующие на М.С. могут быть как внешними () так и – внутренними силами взаимодействия между точками внутри системы () (Рис. 1.2.),

По аксиоме динамики, изложенной в ч. III конспекта, всякому действию соответствует равное и противоположно направленное противодействие.Согласно этой аксиоме(Рис.1.2,в) силы = – и + Распространяя это на любое число “ n ”точек М.С. приходим к выводу, что главный вектор внутренних сил любой М.С. равен нулю, т.е.:

(1.1)

Этим важным свойством внутренних сил мы будем пользоваться очень часто в дальнейшем.

Точки М.С. в их движении под действием как внешних, так и внутренних сил совершают эти перемещения в зависимости от вида внешних и внутренних связей, на них наложенных. Число таких возможных (виртуальных) перемещений всегда равно числу “S” степеней свободы рассматриваемой механической системы.

Виртуальные перемещения точек М.С. можно взять бесконечно малыми и оценивать их соотношения исходя из того, что, например, хорда, стягивающая дугу реальной криволинейной траектории точки, может быть приравнена по длине к длине этой дуги.

Здесь важны не величины виртуальных перемещений точек М.С., а их соотношения.

1.2. Принцип возможных перемещений.

Формулировка.Для того, чтобы механическая система материальных точек находилась в равновесии, необходимо и достаточно, чтобы сумма элементарных работ всех внешних сил, действующих на М.С. была бы не больше нуля на любых возможных (виртуальных) перемещениях “S” этой системы, т.е.